Что такое развертка конуса и как ее построить? формулы и пример решения задачи

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ Р 50017-92 (ИСО 575-78) Машины текстильные и оборудование вспомогательное. Патроны конические переходные. Половина угла конуса 4°20′. Размеры и методы контроля

ГОСТ Р 50018-92 (ИСО 324-78) Машины текстильные и оборудование вспомогательное. Патроны конические для крестовой намотки при крашении (крестовая намотка). Половина угла конуса 4°20′. Размеры и методы контроля

ГОСТ Р 50042-92 (ИСО 368-82) Машины текстильные и оборудование вспомогательное. Патроны для веретен кольцепрядильных и крутильных машин. Конус 1:38 и 1:64. Размеры

ГОСТ Р 50213-92 (ИСО 5237-78) Машины текстильные и оборудование вспомогательное. Патроны конические для намотки пряжи (крестовая намотка). Половина угла конуса 5°57′. Размеры и методы контроля

ГОСТ Р 50663-99 (ИСО 8382-88) Аппараты искусственной вентиляции легких для оживления. Общие технические требования и методы испытаний

ГОСТ 2.320-82 Единая система конструкторской документации. Правила нанесения размеров, допусков и посадок конусов

ГОСТ 8032-84 Предпочтительные числа и ряды предпочтительных чисел

ГОСТ 15945-82 Конусы внутренние и наружные конусностью 7:24. Размеры

ГОСТ 22967-90 Шприцы медицинские инъекционные многократного применения. Общие технические требования и методы испытаний

ГОСТ 24264-93 (ИСО 5356-1-87) Аппараты ингаляционного наркоза и искусственной вентиляции легких. Соединения конические. Часть 1. Конические патрубки и гнезда

ГОСТ 25557-2006 (ИСО 296-91) Конусы инструментальные. Основные размеры

Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.

Колпак на трубу дымохода — своими руками, чертеж и цена

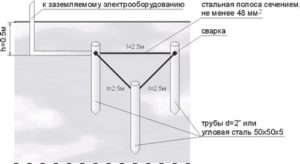
Украшение дымоходов художественно оформленными и совсем простыми колпаками – давняя русская традиция. Особенно это бросается в глаза при посещении дачных кооперативов. Даже трубы самых скромных домиков украшены резными навершиями и флюгарками.

Это устройство не только украшение – оно имеет и чисто функциональное назначение и не одно.

Колпак – не единственное наименование этих устройств, они могут называться также:

• зонт на дымоход;
• грибок на дымоход;
• дымник;
• оголовок
• навершие;

Разумеется, это не полный перечень. Есть еще много разных обозначений.

Похожая конструкция еще называется «флюгаркой», говоря как о подставке для флюгера.

Однако, прежде всего, важно функциональное назначение этих устройств:

1. Защита дома от влаги различного происхождения.
2. Защита дымохода от попадания внутрь посторонних предметов, птиц, мусора и прочее.
3. Усиление тяги в дымоходе за счет целевого направления воздушных потоков.

Навершие на трубу дымохода может быть устроено в виде зонтика или домика с различными формами крыш, может быть вообще представлено в виде причудливых сооружений. Лишь бы оно исполняло свои защитные и вспомогательные функции.

Флюгарка

Конструкция колпаков зависит от формы трубы, которая может быть квадратной, прямоугольной или круглой. Также, имеет значение форма крыши, углы наклона ее элементов и даже господствующее направление ветровых потоков («роза ветров»).

Колпаки условно можно разделить на такие виды:

1. Стандартная флюгарка (напоминает домик с 4 скатной крышей).
2. Зонтик на трубы дымохода – применяется как навершие для круглых дымовых труб.
3. Колпак на трубу дымохода с плоским навершием.
4. Флюгарки с щипцовой крышей.
5. Колпак с полукруглой крышей.
6. Колпак с открывающейся крышкой.

Возможны различные конструктивные решения для колпаков, применяются различные материалы для их изготовления. Но важна их защитная функция от попадания в трубу снега, воды, посторонних предметов, птиц.

Материалы для изготовления

Для изготовления колпаков применяются различные листовые материалы. В ряде случаев, применяются остатки материалов кровли (фальцевой), где применяются листовые кровельные материалы.

Основными материалами для колпаков являются:

• листовая сталь;
• листовой алюминий;
• медный лист;
• лист из нержавеющей стали;
• лист их цинко-титанового сплава;

Долговечность применяемых материалов различна. Колпаки из стали служат обычно от 2 до 5 лет. Листовой алюминий – 5-8 лет. Наиболее долговечны навершия из нержавеющей стали, меди и цинко-титанового сплава. Срок их службы может достигать 50 – 100 лет.

Медные колпаки с плоскими крышами обычно применяют на трубах домов, построенных в стиле «модерн». Для дома в европейском стиле, устанавливают колпаки с полукруглым навершием.

Колпаки с щипцовой крышей применяют в случаях, когда дымовая труба выполняет еще и функцию вентиляционной. Навершия с открывающейся крышкой удобны для чистки дымовой трубы от сажи. Чаще всего, такая необходимость возникает при использовании в качестве топлива дров или торфяных брикетов.

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Формула для определения конусности

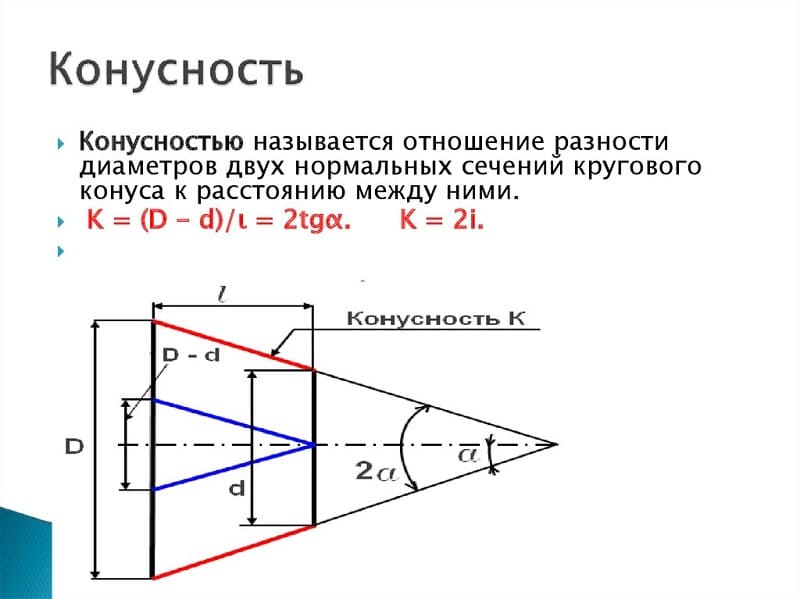
Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Уклон

Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона. Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.

Рис. 6.40. Определение величины уклона

На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5.

Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41).

Рис. 6.41. Построение уклонов и нанесение их величин

При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.

Рис. 6.42. Построение линии по заданному уклону

Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон.

Формула расчета угла конуса

ГОСТ Р 53440-2009(ИСО 1119:1998)

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Основные нормы взаимозаменяемости

ХАРАКТЕРИСТИКИ ИЗДЕЛИЙ ГЕОМЕТРИЧЕСКИЕ

Нормальные конусности и углы конусов

Basic norms of interchangeability. Geometrical product specifications. Standard rates of taper and cone angles

ОКС 17.040ОКСТУ 0074

Дата введения 2012-01-01

Сведения о стандарте

1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский и конструкторский институт средств измерений в машиностроении» (ОАО «НИИизмерения») на основе собственного аутентичного перевода на русский язык стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 242 «Допуски и средства контроля»

4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 1119:1998 «Геометрические характеристики изделий. Ряды конусностей и углов конусов» (ISO 1119:1998 «Geometrical product specifications (GPS) — Series of conical tapers and taper angles», MOD).

При этом в него не включено приложение А (справочное) «Связи в матричной системе GPS» применяемого международного стандарта, которое нецелесообразно применять в национальной стандартизации в связи с тем, что оно содержит сведения о матричной модели Системы стандартов ИСО «Геометрические характеристики изделий (GPS)» и месте применяемого международного стандарта в ней, не относящиеся к объекту стандартизации.

В настоящий стандарт относительно применяемого международного стандарта внесены следующие технические отклонения:

— «Библиография» приведена в соответствие с содержанием стандарта и требованиями ГОСТ Р 1.5-2004.

Указанное приложение, не включенное в настоящий стандарт, приведено в дополнительном приложении ДА.

— ссылки на международные стандарты ИСО заменены ссылками на соответствующие национальные стандарты Российской Федерации согласно таблице А.1 приложения ДБ;

Наименование настоящего стандарта изменено относительно наименования применяемого международного стандарта для приведения в соответствие с требованиями ГОСТ Р 1.5-2004 (пункт 3.5)

5 ВВЕДЕН ВПЕРВЫЕ

Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок — в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Задача на определение диаметра через известную площадь конуса и его образующую

Дан конус, площадь поверхности которого составляет 150 см 2 . Генератриса равна 14 см. Чему равен диаметр конуса?

Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:

r 2 + 14*r — 150/3,14 = 0

При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:

D = 14 2 — 4*1*(-150/3,14) = 387,0828

Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:

Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:

r = (-14+√387,0828)/2 = 2,837 см

Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.

В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.

Нормальные углы и конусы инструментов

НОРМАЛЬНЫЕ УГЛЫ ( ГОСТ 8908-81 )

&nbsp Таблица не распространяется на угловые размеры конусов. При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.

НОРМАЛЬНЫЕ КОНУСНОСТИ и УГЛЫ КОНУСОВ ( ГОСТ 8593-81 )

&nbsp Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.

&nbsp Примечание. Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.

КОНУСЫ ИНСТРУМЕНТОВ УКОРОЧЕННЫЕ ( ГОСТ 9953-82 )

&nbsp Стандарт распространяется на укороченные инструментальные конусы Морзе.

&nbsp *z — наибольшее допускаемое отклонение положения основной плоскости, в которой находится диаметр D от теоретическогот положения. &nbsp ** размеры для справок.

КОНУСНОСТЬ НАРУЖНЫХ И ВНУТРЕННИХ КОНУСОВ И КОНУСОВ С РЕЗЬБОВЫМ ОТВЕРСТИЕМ

РЕКОМЕНДУЕМЫЕ РАЗМЕРЫ ЦЕНТРОВОГО ОТВЕРСТИЯ УКОРОЧЕННОГО КОНУСА

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ НАРУЖНЫЕ( ГОСТ 25557-2006 )

&nbsp Профиль резьбового отверстия соответствует отверстию центровому форма Р по ГОСТ ГОСТ 14034-74.

&nbsp В ГОСТ 25557-2006 все размеры центрового отверстия приводятся в общей таблице. Стандарт также определяет размеры пазов канавок и отвестий, необходимых для конструирования конусов, в случае подачи смазочно-охлаждающей жидкости (СОЖ) через инструмент.

&nbsp В зависимости от конструкции инструментальный хвостовик может иметь соответствующее обозначение:

BI — внутренний конус с пазом; BE — наружный конус с лапкой; AI — внутренний конус с отверстием по оси; АЕ — наружный конус с резьбовым отверстием по оси; BIK — внутренний конус с пазом и отверстием для подачи СОЖ; ВЕК — наружный конус с лапкой и отверстием для подачи СОЖ; AIK — внутренний конус с отверстием по оси и отверстием для подачи СОЖ; АЕК — наружный конус с резьбовым отверстием по оси и отверстием для подачи СОЖ.

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ ВНУТРЕННИЕ( ГОСТ 25557-2006 )

КОНУСЫ ВНУТРЕННИЕ И НАРУЖНЫЕ КОНУСНОСТЬЮ 7 : 24 ( ГОСТ 15945-82 )

&nbsp Допуски конусов внутренних и наружных конусностью 7:24 по ГОСТ 19860-93.

КОНУСЫ ИНСТРУМЕНТОВ Предельные отклонения угла конуса и допуски формы конусов ( ГОСТ 2848-75 )

&nbsp Степень точности инструментальных конусов обозначается допуском угла конуса заданной степени точности по ГОСТ 8908-81 и определяется предельными отклонениями угла конуса и допусками формы поверхности конуса, числовые значения которых указаны ниже.

&nbsp Примечания: &nbsp 1. Отклонения угла конуса от номинального размера располагав в «плюс» — для наружных конусов, в «минус» — для внутренних. &nbsp 2. ГОСТ 2848-75 для наружных конусов предусматривает также степени точности АТ4 и АТ5. Допуски по ГОСТ 2848-75 распространяются на конусы инструментов по ГОСТ 25557-2006 и ГОСТ 9953-82.

&nbsp Пример обозначения конуса Морзе 3, степени точности АТ8:

Морзе 3 АТ8 ГОСТ 25557-2006

&nbsp То же метрического конуса 160, степени точности АТ7:

Метр. 160 АТ7 ГОСТ 25557-2006

&nbsp То же укороченного конуса В18, степени точности АТ6:

Морзе В18 АТ6 ГОСТ 9953-82

ГОСТ 2848-75 — Конусы инструментов. Допуски. Методы и средства контроля ГОСТ 7343-72 — Конусы инструментов с конусностью 1:10 и 1:7. Размеры ГОСТ 10079-71 — Развертки конические с коническим хвостовиком под конусы Морзе. Конструкция и размеры ГОСТ 22774-77 — Конусы и трубки шлифовальные. Типы и размеры ГОСТ 25548-82 — Основные нормы взаимозаменяемости. Конусы и конические соединения. Термины и определения

Как согнуть конус из металла своими руками

Соединение краев тонкого листового металла производится чаще всего в замок — посредством зажимания одного края в другой, но изредка применяются и другие способы, которые в работах юного мастера как раз могут понадобиться чаще. Способы эти вот какие.

Края листов можно просто спаять. Понятно, что это будет самый непрочный способ, особенно, если листы металла тонки. Это будет соединение в притык (1). Такое соединение может быть применено там, где не требуется прочности, но необходимо незаметное соединение. В более толстых листах соединение в притык делается зубцами (2). Так поступают, собственно, уже не жестяники, а медники — мастера, изготовляющие медную посуду, баки, трубы, колпаки и т. п. Соединение в притык можно сделать более прочным, припаяв с внутренней стороны пластинку (3). Это будет притык с накладкой. Более прочное соединение — в нахлестку (4). Один край накладывается на другой, шов пропаивается или скрепляется заклепками. Но это соединение уже имеет выступающий край, что не всегда удобно. Можно отогнуть кромки у одного края и у другого, зацепить их и сжать ударами киянки. Это уже будет простой замок (5).

Наиболее употребительный способ соединения — это двойной замок (6). Он делается так. У одного куска отгибается кромка под прямым углом, у второго кромка также отгибается, но в другую сторону, и прижимается к куску, а затем эта кромка отгибается под Прямым углом в обратную сторону. Обе отогнутых кромки соединяются между собой, загибаются в сторону первой кромки, и шов проколачивается киянкой. С обратной стороны он будет глаже, что надо учитывать при соединениях этим способом. Последовательный ход работы схематически изображен на следующем рисунке:

Двойной замок (схема)

Всевозможные жестяницкие изделия чаще всего соединены двойным замком.

Изредка жестяники применяют соединение при помощи заклепок. Однако этот способ чаще применяется тогда, когда надо приклепать ручку, ушко, полосу и т. п. Изредка заклепками укрепляют швы в накладку и простым замком. Заклепывают обычно мелкими заклепками, лучше с широкими плоскими шляпками, холодным способом. В грубых работах жестяники предпочитают заклепки, свернутые из кусочка жести. Для их изготовления надо иметь кусок железа с дырками разных диаметров, или заклепочник. Ромбовидный кусочек жести свертывают фунтиком при помощи молотка или круглогубцев, вставляют в заклепочник, в дыру подходящего диаметра, и расклепывают головку. Такие заклепки мягки, но, конечно, не имеют того аккуратного вида, как у сплошных заклепок.

Заклепка из жести

Почти все работы с тонким металлом основаны на пластичности металла, его способности изгибаться и расплющиваться. Но мастер должен умело пользоваться своим инструментом, иначе эти же свойства пойдут во вред работе. Как и почему, дальше будет видно.

Развертка усеченного конуса

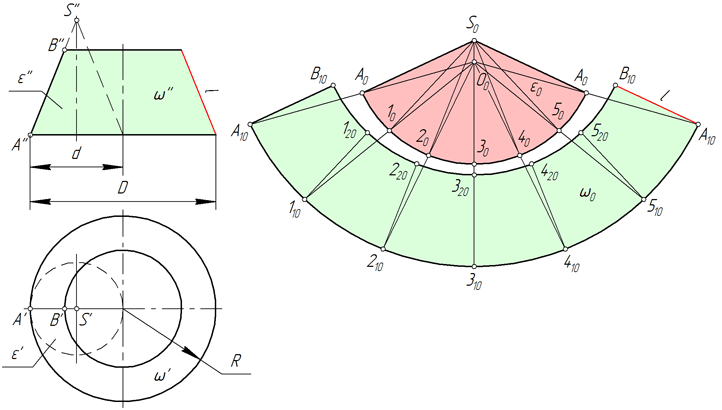
Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.

Алгоритм

1. Строим вспомогательный конус ε, подобный конусу ω, как это показано на рисунке выше. Для удобства построения величину диаметра d выбираем таким образом, чтобы соотношение t=D/d выражалось целым числом. В рассматриваемом примере t=2.
2. Строим развертку боковой поверхности конуса ε – S0A01020304050A0 и на биссектрисе угла A0S0A0 отмечаем точку O0, выбрав ее расположение произвольно.
3. Проводим прямые O0A0, O010, O020, O030, O040, O050, O0A0 и на них откладываем отрезки =t×|O0A0|, = t×|O010|, =t×|O020|, =t×|O030|, =t×|O040|, =t×|O050|, =t×|O0A0| соответственно, где t=D/d. Соединяем точки A10, 110, 210, 310, 410, 510, A10 плавной линией.
4. Из точек A10, 110, 210, 310, 410, 510, A10 проводим лучи, которые параллельны соответственно прямым A0S0, 10S0, 20S0, 30S0, 40S0, 50S0, A0S0, и на них откладываем отрезки A10B10, 110120, 210220, 310320, 410420, 510520, A10B10, равные l – образующей усеченного конуса. Проводим линию B10120220320420520B10.

Какими могут быть поделки из конусов?

Собака

Скрутите половинку круга из коричневой бумаги в конус – туловище готово. Добавьте собачьи ушки, мордочку, лапы и глаза и получится симпатичный песик, а главное – совсем простой в создании.

Слон

Основа, то есть туловище слона – серый тонкий конус из четвертой части круга. Плюс голова с большими ушами, плавно перетекающая в хобот, ноги и хвост. Все просто и быстро, тем более что в помощь прилагается шаблон головы.

Простой бумажный кот

Простейшая поделка, состоит из черного конуса и цилиндрической небольшой головы, прикрепленной на вершине конуса. также понадобятся торчащие ушки, удлиненные глаза, нос, усы, лапы и хвост. Коты в этой технике смотрятся оригинально, красивы в различных расцветках.

Лев

Работа интересна не только конусным туловищем, но и головой, грива вокруг которой из тонких бумажных полосок, склеенных в петли. Часто таким способом мастерят цветы.

Ворона

Из конуса можно сделать забавную ворону или вороненка. Причем работа очень простая. Основа – черный конус, крылья единым целым и голова в виде круга. А также понадобится из желтой бумаги широкий клюв и лапы в виде полос бумаги, сложенных в гармошку.

Бумажные пингвины

Работа настолько простая, что за считанные минуты можно сделать целое семейство пингвинов, с мамой, папой и малышами. Дети быстро запоминают последовательность действий и с легкостью справляются с заданием.

Дракон Беззубик

В продолжении черных персонажей, представляю вам симпатягу Беззубика из мультфильма «Как приручить дракона». Он также состоит из конусного туловища и дополняющих бумажных частей, для создания которых в помощь есть шаблон.

Лягушка

Отличная поделка из конуса, максимально простая. Туловище – широкий зеленый конус, плюс минимум дополняющих деталей в виде четырех одинаковых лап, глаз и языка. Все.

Яркие бабочки

Поделка очень похожа на предыдущую, отличается только формой крыльев и расцветками. Такую бабочку предельно легко сделать, главное — наличие цветной бумаги различных оттенков и собственная фантазия.

Свинка из конуса

Простейшая поделка для детей, даже самых маленьких. Возможно, им понадобится небольшая помощь в создании конуса, а с остальными составляющими они справятся с удовольствием и без проблем.

Конусные курочки

Здесь конус не в оригинальном своем виде, так как при его свертывании нужно оставить кончики. Но все равно техника одинаковая, курочки сделать легко, как и все поделки из конусов.

Божья коровка

Скорее всего, это кулек-сюрприз в виде божьей коровки, с который можно положить сладости и презентовать такой подарок маме. Беря за основу конус, можно сделать такой сюрприз в виде самых разных персонажей.

Поэтапный инструктаж смотрите .

Ведьмочка

Из конуса можно сделать не только животных. В данном варианте – это ведьма, но также это могут быть любые человечки, сказочные персонажи, например, звездочет, лесные феи, гномы, и даже снеговик.

Ежик

Посмотрите, какого можно сделать замечательного ежика! Причем еж полностью состоит из конусов, только некоторые из них разрезанные, чтобы получилось подобие иголок. И сам он не в вертикальном положении, как предыдущие поделки из конусов, а горизонтальном.

Для новогоднего оформления квартиры очень хорошо подходят маленькие ёлочки из подручных материалов. Один из главных плюсов таких ёлочек – простота изготовления и широкое поле для фантазии при их украшении. Кроме того, таких ёлочек можно сделать сразу много – разных по виду и украшению и расставить по всей квартире, таким образом, оригинально украсив её. Проще всего сделать ёлочку-конус из бумаги. На специализированных сайтах есть множество идей украшения таких ёлок, к которым Вы всегда сможете добавить свою авторскую выдумку. При всём разнообразии моделей, основа у всех ёлочек одна – конус из бумаги или картона.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Особенности построения уклона и конусности

Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.

Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.

К особенностям построения угла и конусности можно отнести следующие моменты:

1. Основные линии отображаются более жирным начертанием, за исключением случая, когда на поверхности находится резьба.
2. При проведении работы могут применяться самые различные инструменты. Все зависит от того, какой метод построения применяется в конкретном случае. Примером можно назвать прямоугольный треугольник, при помощи которого выдерживается прямой угол или транспортир.
3. Отображение основных размеров проводится в зависимости от особенностей чертежа. Чаще всего указывается базовая величина, с помощью которой определяются другие. На сегодняшний день метод прямого определения размеров, когда приходится с учетом масштаба измерять линии и углы при помощи соответствующих инструментов практически не применяется. Это связано с трудностями, которые возникают на производственной линии.

В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.

В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.

Основные определения

Прямой круговой конус образован вращением прямоугольного треугольника вокруг одного катета. Как видно, понятие конуса не изменилось со времен Евклида.

Гипотенуза AS прямоугольного треугольника AOS при вращении вокруг катета OS образует боковую поверхность конуса, поэтому называется образующей. Катет OS треугольника превращается одновременно в высоту конуса и его ось. Точка S становится вершиной конуса. Катет AO, описав круг (основание), превратился в радиус конуса.

Если сверху провести плоскость через вершину и ось конуса, то можно увидеть, что полученное осевое сечение представляет собой равнобедренный треугольник, в котором ось является высотой треугольника.

Также часто требуется рассчитать площадь боковой поверхности тела вращения. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.

где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.

Вы здесь

ОБРАБОТКА КОНИЧЕСКИХ ПОВЕРХНОСТЕЙ

§ 1. Общие сведения 1. Область применения конусов. Наряду с цилиндрическими деталями в машиностроении получили довольно широкое распространение детали с коническими поверхностями. Примерами их могут служить конусы центров, хвостовиков сверл, зенкеров, разверток. Для крепления этих инструментов передние участки отверстий шпинделя и пиноли токарного станка имеют также коническую форму. Однако область использования конусов не ограничивается режущими инструментами. Конические поверхности имеют многие детали машин. Широкое использование конических соединений объясняется рядом их преимуществ. 1. Они обеспечивают высокую точность центрирования деталей. 2. При плотном соприкосновении пологих конусов получается неподвижное соединение. 3. Изменяя осевое положение деталей конического соединения, можно регулировать величину зазора между ними. 2. Конус и его элементы. Конус представляет собой геометрическое тело, поверхность которого получается вращением прямой линии (образующей), наклонно расположенной к оси вращения (рис. 129, а). Точка пересечения образующей с осью называется вершиной конуса. Плоскости, перпендикулярные к оси конуса, называются, основаниями. Различают полный и усеченный конусы. Первый расположен между основанием и вершиной, второй — между двумя основаниями (большим и меньшим). Конус характеризуется следующими элементами: диаметром большего основания D; диаметром меньшего основания d; длиной l; углом уклона а между образующей и осью конуса; углом конуса 2а между противоположными образующими. Кроме этого, на рабочих чертежах конических деталей часто употребляют понятия конусность и уклон. Конусностью называется отношение разности диаметров двух перечных сечений конуса к расстоянию между ними. Она опреляется по формуле Уклоном называется отношение разности радиусов двух поперечных сечений конуса к расстоянию между ними. Его определяют по формуле Из формул (9) и (10) видно, что уклон равен половине конусности. Тригонометрически уклон равен тангенсу угла уклона (см. рис. 129, б, треугольник ABC), т. е. На чертеже (рис. 130) конусность обозначают знаком <, а уклон —, острие которых направляется в сторону вершины конуса. После знака указывается отношение двух цифр. Первая из них соответствует разности диаметров в двух принятых сечениях конуса, вторая для конусности— расстояние между сечениями, для уклона — удвоенной величине этого расстояния. Конусность и уклон иногда записываются числами десятичной дроби: 6,02; 0,04; 0,1 и т. д. Для конусности эти цифры соответствуют разности диаметров конуса на длине 1 мм, для уклона — разности радиусов на этой же длине. Для обработки полного конуса достаточно знать два элемента: диаметр основания и длину; для усеченного конуса — три элемента: диаметры большего и меньшего оснований и длину. Вместо одного из указанных элементов может быть задан угол наклона а, уклон или конусность. В этом случае для определения недостающих размеров пользуются вышеприведенными формулами (9), (10) и (11). Пример 1. Дан конус, у которого d=30 мм, /=500 мм, К=1: 20. Определить больший диаметр конуса. Решение. Из формулы (9) Пример 2. Дан конус, у которого D=40 мм, l = 100 мм, а=5 , Определить меньший диаметр конуса. Решение. Из формулы (11) По таблице тангенсов находим tg5°=0,087. Следовательно, d=40—2*100Х Х0,87=22,6 мм. Пример 3. Определить угол уклона а, если на чертеже указаны размеры конуса: D—50 мм, d=30 мм, /=200 мм. Решение. По формуле (11) Из таблицы тангенсов находим а=2 50 . Пример 4. Дан конус, у которого D=60 мм, /=150 мм, К=1 : 50. Определить угол уклона а. Решение. Так как уклон равен половине конусности, можно записать: По таблице тангенсов находим а=0 30 . 3. Нормальные конусы. Конусы, размеры которых стандартизованы, называются нормальными. К ним относятся конусы Морзе, метрические, конусы для насадных разверток и зенкеров с конусностью 1:50 0, под конические штифты — с конусностью 1:50, для конических резьб с конусностью 1 : 16 и др. Наибольшее распространение в машиностроении получили инструментальные конусы Морзе и метрические, основные размеры которых приведены в табл. 13.

Размеры конусов Морзе выражаются дробными числами. Это объясняется тем, что впервые стандарт на них был принят в дюймовой системе измерения, которая сохранилась до настоящего времени. Конусы Морзе имеют различную конусность (примерно 1 20), метрические конусы одинаковую — 1:20. Автор — nastia19071991