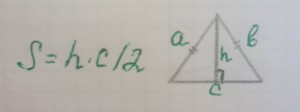Как определить площадь четырехугольника

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

1. Калькулятор для проведения вычислений. 
2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров. 
3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей. 
4. Также потребуется бумага и карандаш для ведения записей в процессе работы. 

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон. 

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение. 
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило. 

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.
 

Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

• Определяется площадь стены без учёта двери или окна. 
• Вычисляется площадь каждого окна или двери путём умножения их длины на ширину. 
• Из площади стены вычитают площадь окон и дверей. 

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их. 

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении. 

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Для чего необходимо знать площадь комнаты и что потребуется для расчетов?

В каких же случаях необходимо рассчитывать площадь комнаты?

Конечно, в первую очередь для определения количества расходных материалов для ремонта. Многие закупают их с запасом, а излишки возвращают в магазин. Однако в данном случае теряется много времени, к тому же не все магазины предоставляют такую услугу. Поэтому целесообразней правильно высчитать площадь всех поверхностей перед покупками.

Чтобы у вас не осталось много обрезков, правильно рассчитайте площадь стен, которые требуют оклейки

• Кроме того, зная площадь, проще распланировать свой бюджет. Ведь даже стоимость работ наемных работников в большинстве случаев зависит от того, сколько квадратных метров они должны обработать.
• Количество осветительных приборов также зависит от площади. Однако в большинстве случаев к сложным расчетам при выборе светильников не прибегают, данный вопрос обычно решается опытным путем.

Пример недостаточного освещения в ванной комнате

И последнее. Одна из главных величин в квартире – объем помещений (при этом необходимо площадь умножить на высоту), ведь в зависимости от него подбирают климатическое оборудование.

Мощность кондиционера в первую очередь зависит от объема помещения

Таким образом, существует огромное количество причин, по которым необходимо правильно высчитать площадь помещения. Но с чего же начать? Сначала нужно подготовить измеряемое помещение и инструменты.

Измерения желательно проводить в полностью освобожденном помещении. Если такой возможности нет, расчистите хотя бы участки около стен, ведь именно вдоль них будут проводиться замеры.

Обязательно отодвиньте всю крупную мебель от стен, которые вы будете измерять

Итак, для определения площади помещения необходимы следующие приспособления:

1. Рулетка. Конечно, электронное приспособление удобней, но оно имеет большую погрешность. Кроме того, такой рулеткой не измерить сложные формы, при работе с выступающими элементами также могут возникнуть проблемы. Поэтому оптимальный набор – простая рулетка и линейка. Главное – проверить их точность, так как многие старые или детские приспособления имеют приличную погрешность.
2. Карандаш.
3. Листок бумаги для вычислений и записи результатов.
4. Калькулятор.

Кроме того, вам может понадобиться длинная линейка для проверки ровности стен.

Как посчитать площадь комнаты: методика расчета по полу

Можно рассчитать площадь пола. Данная процедура состоит из таких этапов. Прежде всего, необходимо освободить стены помещения. Лучше проводить измерения в пустом помещении. Если помещение прямоугольное, то можно перемножить две стороны

В реальности стороны могут немного отличаться, поэтому так важно мерить все стороны. В некоторых случаях комната может быть не правильной конфигурации

В такой ситуации все пространство делится на отдельные прямоугольники. При этом можно нарисовать схему со всеми размерами. Затем считается площадь отдельных участков. Кстати, помещение не обязательно будет состоять только из прямоугольников. Оно может содержать треугольники и даже круги.

В таблице можно посмотреть соответствие площади на полу с показателями для стен при определенной высоте потолка

Если вы не знаете, как посчитать квадратные метры комнаты, то можно воспользоваться специальным калькулятором. При вычислении габаритов не обязательно соблюдать все размеры до сантиметра. Часто применяется округление значений. Иногда  требуется учитывать разные углубления и выступы в стенах.

При расчетах важно учитывать и их предназначение. Если нужно узнать значения для монтажа теплого пола, то можно не учитывать пространство, занятое тяжелой мебелью

Есть варианты, когда в помещении используются разные уровни пола. В подобной ситуации также требуется поделить комнату на отдельные зоны. Не стоит осуществлять замеры по стене, так как она может иметь кривую поверхность.

Сложно определить площадь по полу, имеющего разнообразные выступы в виде волн или полукругов.

Полы сложной конфигурации требуют особой внимательности и использования специальных формул

Нахождение площади четырёхугольника различными способами и методами

Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).

Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.

Теперь пусть даны стороны и противолежащие углы четырёхугольника.

Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).

На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.

Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.

Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.

Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.

Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:

S = ((a + b+ c + d)/2)*r

Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:

S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.

Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.

Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:

S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.

Определение площади участка на ПКК

Публичная кадастровая карта (ПКК) — это онлайн-сервис, с помощью которого любой гражданин может узнать основные характеристики любого земельного участка, помещенные в кадастр недвижимости (ЕГКН).

Для того, чтобы узнать величину площади с помощью ПКК, надо зайти на страницу http://pkk5.rosreestr.ru и найти участок на карте. Для этого используется специальное меню, которое позволяет определить участок по кадастровому номеру, адресу.

Так, введя в поисковую систему ПКК адрес участка, можно получить его расположение на карте и некоторые данные.

Среди этих данных имеется площадь данного участка, которая является официальной величиной, так как она введена в ЕГРН.

Необходимо отметить, что не все участки земли можно таким образом найти по адресу. Например, при нахождении участка c кадастровым номером 50:38:0050302:130 в таблице его параметров указан адрес: «обл. Московская, р-н Зарайский, снт «Изобретатель», уч-к 116″.

на других страницах.

Это говорит о том, что система поиска земельного участка на ПКК по адресу не до конца отработана Росреестром.

Чтобы определить площадь участка по координатам, вначале необходимо узнать эти координаты. Если участок уже найден на карте, то приблизительные координаты характерных точек можно определить, подводя к ним курсор. По этим координатам, в дальнейшем, можно определить площадь участка по формуле для аналитического метода.

Более точно координаты характерных точек участка можно узнать только при платном заказе выписки из ЕГРН для этого участка.

По новому закону в связи с объединением баз данных ЕГРП и ЕГРН такая выписка с 1.01 2017 года заменяет собой свидетельство на объект недвижимости, кадастровый паспорт, кадастровую выписку и выписку из ЕГРП. То есть, выписка из ЕГРН является основным документом на недвижимость.

https://youtube.com/watch?v=JGe6f6Qm60E

Формулы для нахождения площади

Через две стороны

Площадь прямоугольника через две стороны можно вычислить по формуле:

\(S=ab\)

где a, b — соседние стороны прямоугольника.

Через диагонали и синус угла между ними

Для того, чтобы найти площадь прямоугольника через диагонали и синус угла, нужно воспользоваться формулой:

\(S=\frac{d^2\sin\alpha}2\)

где \(d \) — диагональ, \(\alpha\) — угол между диагоналями (острый).

Через любую сторону и диагональ

Чтобы определить площадь прямоугольника через любую сторону и диагональ, нужно воспользоваться формулой:

\(S=a\sqrt{d^2-a^2}=b\sqrt{d^2-b^2}\)

где a, b — соседние стороны прямоугольника, d — диагональ.

Через сторону и диаметр описанной окружности

Чтобы узнать площадь прямоугольника через сторону и диаметр описанной окружности, нужно воспользоваться формулой:

\(S=a\sqrt{D^2-a^2}=b\sqrt{D^2-b^2}\)

где a, b — соседние стороны прямоугольника, D — диаметр описанной окружности.

Через сторону и радиус описанной окружности

Вычисление площади прямоугольника через сторону и радиус описанной окружности происходит по формуле:

\(S=a\sqrt{4R^2-a^2}=b\sqrt{4R^2-b^2}\)

где a, b — соседние стороны прямоугольника, R — радиус описанной окружности.

Через сторону и периметр

Чтобы посчитать площадь прямоугольника через сторону и периметр, нужно воспользоваться формулой:

\(S=\frac{Pa-2a^2}2=\frac{Pb-2b^2}2\)

где a, b — соседние стороны прямоугольника, Р — периметр.

Через радиус описанной окружности и синус угла между диагоналями

Способ нахождения площади прямоугольника через радиус окружности и синус угла между диагоналями происходит по формуле:

\(S=\frac{4R^2\sin\alpha}2\)

Что такое прямоугольник

Определение

Прямоугольник — параллелограмм, в котором все углы прямые.

В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. 

Свойства

1. Противоположные стороны попарно равны.
2. Диагонали равны. Они пересекаются и точкой пересечения делятся пополам.
3. Биссектриса отсекает от прямоугольника равнобедренный треугольник.
4. Стороны прямоугольника являются его высотами.
5. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.
6. Около любого прямоугольника можно описать окружность, при этом ее диаметр численно равен диагонали прямоугольника.

Признаки

Параллелограмм является прямоугольником при выполнении одного из следующих условий:

1. Диагонали параллелограмма равны.
2. Сумма квадратов соседних сторон параллелограмма равна квадрату диагонали.
3. Все углы параллелограмма равны.

Калькулятор для неправильной фигуры

Очень часто измеряемое пространство имеет очень сложную форму, которую не всегда удается разбить на простые элементы.

Чтобы просто определить такую площадь, стоит воспользоваться интернет-приложением SketchAndCalc. Он является калькулятором площади неправильных фигур для любой формы изображения. Это единственный калькулятор площади, способный вычислять по загруженным изображениям, он имеет уникальную функцию, которая позволяет пользователю установить масштаб чертежа любого изображения, прежде чем рисовать периметр. Таким образом, углы или кривые неправильной фигуры легко вычисляются.

Проще говоря, если есть изображение, которое можно загрузить, или адрес карты для поиска, можете рассчитать площадь неправильной фигуры независимо от того, насколько сложна она, просто рисуя периметр области. Калькулятор может даже суммировать вычисления нескольких площадей вместе путем рисования слоев. После вычисления первой области можно добавить новый слой чертежа, что позволяет выполнить неограниченное количество вычислений области.

Результаты калькулятора площади отображаются в дюймах и метрах, увеличивая его полезность и устраняя необходимость преобразования. Это наряду с точными инструментами рисования и увеличения гарантирует, что площади каждой неправильной фигуры рассчитываются точно. Он также может размещать правильные формы многоугольника с фиксированными углами и точными линиями.

Инструмент с ограниченным рисунком привязывается к общим углам, а линию длины можно редактировать вручную с помощью клавиатуры. Приложение полезно, если измеряемая область имеет прямую сторону или длину. Еще одной уникальной особенностью SketchAndCalc TM является то, что он имеет продвинутый инструмент рисования кривой для неправильных фигур. Некоторые приложения калькулятора области позволяют осуществлять поиск по карте.

SketchAndCalc делает это очень точно, используя поиск по долготе и широте. Независимо от того, находится ли замеряемая область на сельскохозяйственных землях или в море, пользователь будет тратить меньше времени на поиск и больше времени на расчет площади территории. Это универсальная утилита, применяемая во многих отраслях промышленности, в строительстве, садоводстве. Она используется и энтузиастами по благоустройству своего дома и придомовой территории. Калькулятор ландшафта или калькулятор земельной площади также нашел своих пользователей среди землеустроителей. Теперь они знают, как рассчитать площадь участка легко и быстро.

Однако, помимо этих общих применений, многие работающие в области образования, медицины, науки и исследований нуждаются в расчете площади неправильных форм, таких как клеточные мембраны или другие объекты, обнаруженные в биологии, и с удовольствием пользуются этим приложением.

Для применения математики в повседневной жизни недостаточно уметь считать один плюс один. Существенным аспектом окружающей среды являются геометрические структуры, то есть представление повседневных предметов в прямоугольной, квадратной, круглой или треугольной форме. И надо уметь рассчитать нужную площадь.

Кроме того, геометрические фигуры используются и при построении диаграмм, схем, презентаций

Вот почему так важно уметь делать различные расчеты, в том числе и вычисление площади

Определения и соглашения

В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.

1. Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
2. Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
3. Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
4. Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
5. Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
6. Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
7. Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
8. Угол между сторонами a и b будем обозначать следующей записью (a,b).

Погрешность определения площади

При определении площадей участков возникают неточности, которые характеризуются погрешностями. Погрешность — это разность между вычисленной величиной площади участка и ее истинной величиной.

Для различных методов определения площади такие погрешности могут быть различными.

Для аналитического метода точность расчета площади зависит исключительно от погрешностей, связанных с измерением координат поворотных точек. При этом, средняя квадратическая погрешность (СКП) аналитического метода расчета (mp) определяется формулой:

mp= mt*√ P, где:

• mt — СКП расположения поворотных точек;
• P — площадь участка.

Для примера можно взять допустимые при межевании точности mt, которые определены соответствующими нормативными актами (например, Приложением к приказу МЭР № 518). Эти точности зависят от типа земель.

Так, для населенных пунктов этот показатель равен 10 см, а для дачных участков и садоводств-20 см. Таким образом, для садового участка в 600 кв. м точность определения площади аналитическим методом может составить:

mpс= 0,2*√600=4,89 м.

При реализации графического метода на его точность влияют погрешности измерений, погрешности составления плана, деформация бумаги. Относительная погрешность такого метода составляет от 1:500 до 1:1000.

Точность механического метода также зависит от погрешностей составления плана (или карты), состояния бумаги, на которой нанесен план участка. Кроме того, на точность этого метода влияет размер участка. Этот метод не рекомендуется применять для участков размером менее 10-12 см2.

В благоприятных условиях относительная погрешность измерений площади планиметром может достигать 1:400.

Мы расскажем вам о том как взять земельный участок в аренду с правом выкупа.

При покупке квартиры можно получить налоговый вычет. Подробнее об этом читайте в нашей статье.

Хотите оформить в собственность участок, взятый в аренду на 49 лет? Здесь есть подробная инструкция.

Формулы площади треугольника

1. Формула площади треугольника по стороне и высотеПлощадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

   S =	1
   2

2. Формула площади треугольника по трем сторонам

   S = √()()()

3. Формула площади треугольника по двум сторонам и углу между ними
   Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

   S =	1
   2

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности

   S =
   4R

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружностиПлощадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

   S =  ·

   где S — площадь треугольника, — длины сторон треугольника, — высота треугольника, — угол между сторонами и , — радиус вписанной окружности,
   R — радиус описанной окружности,

   =	+  +	— полупериметр треугольника.
   2

Формулы для площадей четырехугольников

Четырехугольник	Рисунок	Формула площади	Обозначения
		S = ab	a и b – смежные стороны
		d – диагональ,φ – любой из четырёх углов между
	S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R	R – радиус ,φ – любой из четырёх углов между
		S = a ha	a – сторона,ha – , опущенная на эту сторону
	S = absin φ	a и b – смежные стороны,φ – угол между ними
		d1, d2 – , φ – любой из четырёх углов между ними
		S = a2	a – сторона квадрата
	S = 4r2	r – радиус
		d – квадрата
	S = 2R2 Получается из верхней формулы подстановкой d = 2R	R – радиус
		S = a ha	a – сторона,ha – , опущенная на эту сторону
	S = a2 sin φ	a – сторона,φ – любой из четырёх углов ромба
		d1, d2 –
	S = 2ar	a – сторона,r – радиус
		r – радиус ,φ – любой из четырёх углов ромба
			a и b – основания,h –
	S = m h	m – ,h –
		d1, d2 – , φ – любой из четырёх углов между ними
		a и b – основания,c и d  – боковые стороны
		S = ab sin φ	a и b – неравные стороны,φ – угол между ними
		a и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.
	S = (a + b) r	a и b – неравные стороны,r – радиус
		d1, d2 –
Произвольный выпуклый четырёхугольник			d1, d2 – , φ – любой из четырёх углов между ними
		,	a, b, c, d – длины сторон четырёхугольника,p – , Формулу называют «Формула Брахмагупты»

	S = ab гдеa и b – смежные стороны
	гдеd – диагональ,φ – любой из четырёх углов между
	S = 2R2 sin φ гдеR – радиус ,φ – любой из четырёх углов между Формула получается из верхней формулы подстановкой d = 2R
	S = a ha гдеa – сторона,ha – , опущенная на эту сторону
	S = absin φ гдеa и b – смежные стороны,φ – угол между ними
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	S = a2 гдеa – сторона квадрата
	S = 4r2 гдеr – радиус
	гдеd – квадрата
	S = 2R2 гдеR – радиус Получается из верхней формулы подстановкой d = 2R
	S = a ha гдеa – сторона,ha – , опущенная на эту сторону
	S = a2 sin φ гдеa – сторона,φ – любой из четырёх углов ромба
	гдеd1, d2 –
	S = 2ar гдеa – сторона,r – радиус
	гдеr – радиус ,φ – любой из четырёх углов ромба
	гдеa и b – основания,h –
	S = m h гдеm – ,h –
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	гдеa и b – основания,c и d  – боковые стороны
	S = ab sin φ гдеa и b – неравные стороны,φ – угол между ними
	гдеa и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.
	S = (a + b) r гдеa и b – неравные стороны,r – радиус
	гдеd1, d2 –
Произвольный выпуклый четырёхугольник
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	, гдеa, b, c, d – длины сторон четырёхугольника,p – Формулу называют «Формула Брахмагупты»

S = ab гдеa и b – смежные стороны

гдеd – диагональ,φ – любой из четырёх углов между

S = 2R2 sin φ гдеR – радиус ,φ – любой из четырёх углов между Формула получается из верхней формулы подстановкой d = 2R

S = a ha гдеa – сторона,ha – , опущенная на эту сторону

S = absin φ гдеa и b – смежные стороны,φ – угол между ними

гдеd1, d2 – , φ – любой из четырёх углов между ними

S = a2 гдеa – сторона квадрата

S = 4r2 гдеr – радиус

гдеd – квадрата

S = 2R2 гдеR – радиус Получается из верхней формулы подстановкой d = 2R

S = a ha гдеa – сторона,ha – , опущенная на эту сторону

S = a2 sin φ гдеa – сторона,φ – любой из четырёх углов ромба

гдеd1, d2 –

S = 2ar гдеa – сторона,r – радиус

гдеr – радиус ,φ – любой из четырёх углов ромба

гдеa и b – основания,h –

S = m h гдеm – ,h –

гдеd1, d2 – , φ – любой из четырёх углов между ними

гдеa и b – основания,c и d  – боковые стороны,

S = ab sin φ гдеa и b – неравные стороны,φ – угол между ними

гдеa и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.

S = (a + b) r гдеa и b – неравные стороны,r – радиус

гдеd1, d2 –

Произвольный выпуклый четырёхугольник

гдеd1, d2 – , φ – любой из четырёх углов между ними

гдеa, b, c, d – длины сторон четырёхугольника,p – Формулу называют «Формула Брахмагупты»

[править] Формулы

Формулы в векторной и координатной форме

Введём обозначения:

\bar r_1=(x_1,y_1,z_1) — радиус-вектор первой точки;

\bar r_2=(x_2,y_2,z_2) — радиус-вектор второй точки;

\bar r_3=(x_3,y_3,z_3) — радиус-вектор третьей точки;

\bar r_4=(x_4,y_4,z_4) — радиус-вектор четвёртой точки;

\bar n=(A,B,C) — нормаль к плоскости, проходящей через три заданные точки;

S_Δ — площадь треугольника, построенного по трём заданным точкам;

S_четыр — площадь четырёхугольника, построенного по четырём заданным точкам.

где

Формула Брахмагупты

Рассмотрим четырёхугольники, вокруг которых можно описать окружность и у которых порядок следования вершин 1, 2, 3, 4. Для нахождения их площади можно использовать формулу Брахмагупты.

Введём обозначения:

a — длина стороны четырёхугольника, расположенной между первой и второй точками;

b — длина стороны четырёхугольника, расположенной между второй и третьей точками;

c — длина стороны четырёхугольника, расположенной между третьей и четвёртой точками;

d — длина стороны четырёхугольника, расположенной между первой и четвёртой точками;

p — полупериметр четырёхугольника, построенного по четырём заданным точкам.

где

• Когда одна из сторон четырёхугольника стремится к нулю, тогда формула Брахмагупты превращается в формулу Герона для площади треугольника.
• Когда четырёхугольник является прямоугольником и a≠b, тогда формула Брахмагупты превращается в формулу площади прямоугольника, S_{прямоуг}=ab, где c=a, d=b, p=a+b.
• Когда четырёхугольник является равнобедренной трапецией и b=d, тогда формула Брахмагупты превращается в формулу площади трапеции, S_{равн.трап}=h(a+c)/2, где h2=(p-a)(p-c), p-b=(a+c)/2.

Один из методов определения площади четырехугольника состоит в разбиении фигуры на два треугольника с помощью диагонали и в вычислении суммы площадей образовавшихся треугольников.