Можно ли вывести ровный внутренний или наружный угол дома в 90 градусов с помощью уголков, цемента или гипсокартона: советы, правила, техники выравнивания правилом

Теорема Пифагора

Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора. Вспомним определение: ”В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов” ( a 2 + b 2 = с 2 ), где a и b – катеты, а с – гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.

А теперь вернемся к нашим замерам и применим теорему на практике.

Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом. Если в результате измерения получилось другое число, то угол не равен 90 градусов.

Показываю 3 способа как быстро построить прямой угол на местности имея любую веревку

Добрый день, уважаемые гости и подписчики канала «Строю для себя»!

Ниже описаны 3 приема восстановления перпендикуляра или построения прямого угла на местности к любой прямой линии. Данные мероприятия очень важны в строительстве при построении осей на плане и при сооружении обноски для дальнейшего возведения фундаментов или стен.

Имея только отрезок любой веревки, шнурки или троса, пользуясь данными способами — вы сможете совершенно точно построить перпендикуляр.

Итак, способ №1: Равнобедренный треугольник

Определяем точку на прямой линии, к которой будем строить перпендикуляр (для наглядности — я в эту точку воткнул шампур

Отмечаем по обе стороны от него две равноудаленные точки (с помощью веревки это очень просто сделать). Теперь мы имеем три точки, которые находятся на одной прямой линии и два равных отрезка между ними (на рисунке ниже — 3 шампура).

Затем, нам достаточно определить середину веревки произвольной длины (В своем случае, для удобства, я на противоположных концах сделал петли, накинул их на колышек (шампур) и натянул веревку, тем самым разделил ее на две равные части).

Теперь, концы веревки совмещаем с двумя крайними точками и натягиваем ее за найденную середину.

Перпендикуляр готов (Свойство равнобедренного треугольника, высота которого делит основание на два равных отрезка)

Способ №2: Пересечение двух дуг

Данный способ выручает, когда у вас есть только короткая веревка. Как и в предыдущем способе, нам требуется опять же построить три точки на одной прямой, где две крайние равноудалены от центральной.

Теперь, подобно циркулю, из каждой крайней точки рисуем дуги одинакового радиуса. Точка пересечения двух дуг и будет давать нам перпендикуляр к прямой.

Схематично, это выглядит так (точка О является точкой пересечения дуг):

Наверное, это самый используемый способ, в котором применяются равные отрезки в соотношении 3:4:5. Данные отрезки могут измеряться в сантиметрах, метрах, километрах или любой произвольной длины, которую мы и будем использовать.

Для наглядности, я сделал на одной веревке 13 узлов с равными расстояниями друг от друга.

Теперь, достаточно просто туго растянуть веревку за вершины, которые отделяются между собой 3, 4 и 5 отрезками. Опять же, использую шампуры :-)))

Прямой угол построен!

На этом всё, спасибо за терпение :-)))

Если Вам было интересно, ставьте палец вверх и подписывайтесь на мой канал! Впереди много интересных тем!

Чем проверять и выставлять углы

Угол легко проверить строительным угольником, можно приобрести в магазине, если собираетесь выводить углы, он будет вам необходим.

Строительный угольник необходим для проверки углов

Просто прислоняем угольник к внутреннему углу. Наружные углы мы пока рассматривать не будем, ради понимания самого процесса. После понимания как выравнивать внутренние углы под 90 градусов своими руками, внешние для вас проблем не составят.

Проверяем внутренний угол

Смотрим, что получается. Если всё нормально, зазоров между угольником нет, то расслабьтесь. Если зазор превышает 5 мм, то следует насторожиться и узнать как выровнять такой угол в прямой, что бы и ванна и шкафы висели хорошо. Дело в том, что зазор в 5 мм под небольшим, пускай полуметровым (в длину хотя бы одной грани) угольником, на всю длину стены оказывается довольно крупным и в конце стены может достичь и 5 см.

Делаем угольник самостоятельно

Угольник можно соорудить и самостоятельно, причём любого размера. Удобнее всего делать такой угольник из гипсокартонных профилей 27*28 мм (жёстких или полужёстких).

Пользуемся пра́вилом египетского треугольника, при котором: если катеты угла равны 3 и 4 частям, а гипотенуза 5 частям, то угол будет прямоугольным (прямой угол между катетами).

Надрезаем и сгибаем нужной длины профиль посредине (стороны нашего угольника не обязательно должны быть равны 3 и 4 определённым нами частям, пра́вило нужно лишь для того, чтобы сделать прямой угол). Сгибаем, принимаем за 1 часть, к примеру, 30 см. Чем больше вы сделаете часть, тем «прямее» получится угол.

Отмеряем на одном катете 3 части — 90 см, на втором 4 части — 120 см. Делаем отметки маркером. Далее, сгибая угол, отмеряем строго от отметок гипотенузу — 5 частей — 150 см. Наш угол прямой, осталось его зафиксировать тем же профилем на саморезы. Тут следует быть аккуратным, чтобы не сбить угол, проверьте правильность разметки несколько раз.

Ниже в ролике наглядно показано как соорудить такой угольник.

Проверяем угол с помощью лазерного построителя плоскостей

Лазерные построители плоскостей позволяют с лёгкостью выверять вертикали, горизонтали, отклонения целых площадей, а так же и углы, если такая функция на нём предусмотрена.

Лазерный построитель плоскостей, с функцией построения прямого угла

Не все построители плоскостей подходят, а те которые проецируют две перпендикулярных вертикальных плоскости. С ним работа гораздо облегчается, но стоит такой прибор начиная от 15 тыс. руб. Можно найти и подешевле, особенно в Китае, но у них могут быть и отклонения, хоть часто и не значительные, они как минимум, написаны в паспорте устройства, а на дешёвых моделях отклонения могут и вовсе не совпадать с паспортными. Проверьте это перед использованием с помощью большого угольника, который описан выше или на заведомо прямых углах.

Такие приборы позволяют не только выводить прямые углы, а так же и → штукатурные плоскости и → стяжку пола (по ссылкам рассказано как делать штукатурку по маякам и цементно-песчаную стяжку).

Лазерный построитель плоскостей (нивелир) стоит лишь включить, приставить к углу и прочертить линии на полу, которые он спроецировал. Далее я расскажу как проверить углы и выстроить прямоугольник на площади помещения с помощью угольника и правила, а как работать лазерным построителем плоскостей станет понятно из этого рассказа.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник»

Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов

Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Зачем нужна разметка

Многие непрофессиональные строители не понимают важности подготовительных работ. Ниже представлены проблемы, которые могут возникнуть, если сделать разметку не правильно или вовсе пренебречь ей:

• нарушение геометрических размеров здания;
• неточности угловых размеров;
• неправильная работа несущих конструкций из-за отклонения фундаментов и стен от проектных;
• при использовании сборных перекрытий их элементы, изготовленные по проектным значениям, могут не подойти по существующим размерам, что приведет к дополнительным финансовым и трудовым затратам.

От расположения фундаментов зависит местоположение будущих стен здания и размеры помещений.

Начинаем разметку от первой стены

Первым делом проверим нашу первую стену на вертикаль и плоскость. Если выравниваем 2 угла, то это стена, параллельная ванне, если выравниваем 4 угла (всю площадь), то стена с проёмом. Если стена завалена, её нужно будет выровнять первым делом, но не торопитесь, ведь мы ещё не проверили всю площадь.

Для начала просто отобьём ровную линию параллельно первой стене, максимально приближённую к ней.

Проведём первую линию, параллельно первой стены

Далее между первой стеной и второй стеной установим угольник одной гранью параллельно первой линии, а на вторую грань угольника накладываем прави́ло. Совмещаем грань прави́ла и угольника, тем самым «удлинняя» наш угольник. Чертим линию на полу до конца стены максимально приближённую к стене. Регулируем и совмещаем наш увеличенный угольник так что бы:

• линия была ровной,
• расстояние до стены минимальным,
• вторая грань угольника была параллельна первой линии.

Так получаем первый прямой угол.

От первой линии отобьём вторую, перпендикулярную ей

Далее идём на следующий угол, до которого мы чертили линию, и совмещаем угольник одной гранью параллельно второй линии. Повторяем процедуру с правилом (совмещаем его с угольником) и чертим третью линию перпендикулярную второй, опять же максимально приближённую к стене.

Тут требуется некоторая сноровка, чтобы совмещать прави́ло, угольник и делать прямой угол с линиями, максимально приближёнными к стене (это делается для того, что бы при штукатурке «не съесть» лишнее пространство). Если прави́ла не хватает, дочерчиваем до куда хватает, переставляем прави́ло, совмещая его с линией, и проводим её до конца стены.

Чертим третью линию перпендикулярную второй

Чертим четвёртую линию, по аналогии. В итоге у нас должен получится начерченный на полу прямоугольник внутри нашего помещения. Проверяем его по первой грани — по стене с проёмом, так же, прикладывая угольник и правило.

Проверяем по 1-й грани полученный прямоугольник

Если всё ровно, можно немного расслабиться. Если нет, повторяем процедуру и/или смотрим где ошиблись.

Показываю 3 способа как быстро построить прямой угол на местности имея любую веревку

Добрый день, уважаемые гости и подписчики канала «Строю для себя»!

Ниже описаны 3 приема восстановления перпендикуляра или построения прямого угла на местности к любой прямой линии. Данные мероприятия очень важны в строительстве при построении осей на плане и при сооружении обноски для дальнейшего возведения фундаментов или стен.

Имея только отрезок любой веревки, шнурки или троса, пользуясь данными способами — вы сможете совершенно точно построить перпендикуляр.

Итак, способ №1: Равнобедренный треугольник

Определяем точку на прямой линии, к которой будем строить перпендикуляр (для наглядности — я в эту точку воткнул шампур

Отмечаем по обе стороны от него две равноудаленные точки (с помощью веревки это очень просто сделать). Теперь мы имеем три точки, которые находятся на одной прямой линии и два равных отрезка между ними (на рисунке ниже — 3 шампура).

Затем, нам достаточно определить середину веревки произвольной длины (В своем случае, для удобства, я на противоположных концах сделал петли, накинул их на колышек (шампур) и натянул веревку, тем самым разделил ее на две равные части).

Теперь, концы веревки совмещаем с двумя крайними точками и натягиваем ее за найденную середину.

Перпендикуляр готов (Свойство равнобедренного треугольника, высота которого делит основание на два равных отрезка)

Способ №2: Пересечение двух дуг

Данный способ выручает, когда у вас есть только короткая веревка. Как и в предыдущем способе, нам требуется опять же построить три точки на одной прямой, где две крайние равноудалены от центральной.

Теперь, подобно циркулю, из каждой крайней точки рисуем дуги одинакового радиуса. Точка пересечения двух дуг и будет давать нам перпендикуляр к прямой.

Схематично, это выглядит так (точка О является точкой пересечения дуг):

Наверное, это самый используемый способ, в котором применяются равные отрезки в соотношении 3:4:5. Данные отрезки могут измеряться в сантиметрах, метрах, километрах или любой произвольной длины, которую мы и будем использовать.

Для наглядности, я сделал на одной веревке 13 узлов с равными расстояниями друг от друга.

Теперь, достаточно просто туго растянуть веревку за вершины, которые отделяются между собой 3, 4 и 5 отрезками. Опять же, использую шампуры :-)))

Прямой угол построен!

На этом всё, спасибо за терпение :-)))

Если Вам было интересно, ставьте палец вверх и подписывайтесь на мой канал! Впереди много интересных тем!

Штукатурка закругленных углов стен своими руками.

Углы с закруглением штукатурить не сложнее, чем обыкновенные:

1. Выравнивание стен. Стены штукатурят и выравнивают по стандартной технологии.
2. Армирование. Эллипс незначительного диаметра не требует арматуры. Но при создании значительных закруглений (при диам. более 10см), их укрепляют армирующей сеткой, проволокой. Можно обойтись вкручиванием шурупов (шаг не менее 20 см).
3. Обрызг.
4. Применение шаблона. Набрасывают раствор и снимают его излишки правилом. В случае с закруглениями роль маяков выполняет поверхность обеих стен, а правила – специально изготовленный шаблон.

Такое искривленное правило делают так: прикладывают к скруглению легко гнущуюся, но прочную проволоку, вдавливают ее в эллипс. Так получают точный рисунок будущего шаблона.

Проволоку прикладывают к фанере (не менее 6мм толщ.) или листовой стали, жести. Обводят карандашом. По этой линии обрезают излишки. Шаблон готов!

Когда штукатурка углов полностью высохнет, наносят последний, накрывочный слой с применением мелкого песка (фракция не более 1мм). Этот слой затирают войлоком, чтобы сделать стену максимально гладкой.

Инструменты

Заранее готовят инструменты и приспособления:

• для наложения, разравнивания состава – шпатели (с лопатками разной ширины);
• для затирания – тёрку или полутёрок;
• для грунтования – кисть, валик;
• для приготовления смеси – миксер и ёмкость;
• чтобы вывести 90–градусный усенок или лузг – уголковый шпатель;
• для армирования – контрашульцы или серпянку;
• для шлифования – наждачку/шлиф-машинку;
• для разметки – карандаш/маркер, угольник, правило, уровень, отвес или лазерный нивелир, шнурок;
• для защиты приграничных деталей – малярный скотч;
• для фиксирования профилей при выравнивании маячками – саморезы, крепёж, отвёртка;
• для выравнивания откосов – малку;
• для очистки кирпичного основания – щётку со стальной щетиной.

В помещении также понадобится стремянка или подмости, плёнка для защиты пола.

Рассмотрим устройство каждого из типов фундамента отдельно

Ленточный фундамент

Разметка фундамента под дом 3х3 м

Ленточный фундамент представляет собой траншеи, заполненные железобетоном, бутобетоном, кирпичом или фундаментными железобетонными блоками. Траншеи копаются непосредственно под стенами.

Материал, используемый для фундамента, зависит от типа грунта:

• Кирпичный фундамент. Используется крайне редко, в основном для наружной части фундамента. Данный тип может быть использован на глиняном грунте. Ни в коем случае нельзя его применять при повышенном уровне грунтовых вод.
• Бутобетон. Применяется на скалистых либо песчаных грунтах.
• Бетонные плиты и литой железобетон используется на глиняных грунтах.

Плюсы данного фундамента заключаются в следующем:

• Подходит для строительства на любом грунте.
• Возможность размещения под постройкой подвала.
• Более дешевый и простой чем плитный.

Ленточный фундамент может быть:

• Мелкозаглубленый. Используется на устойчивых, стабильных грунтах и для строительства легких построек. Глубина траншеи для такого грунта не превышает 70 см, то есть, не проходит глубже уровня промерзания грунта.
• Заглубленный фундамент. Используется только для тяжелых построек. Глубина траншеи для такого грунта проходит дальше уровня промерзания земли. Такой тип фундамента хорош тем, что является устойчивым к сдвигам грунта. Однако только при условии что здание, стоящее на нем будет достаточно тяжелым.
• Монолит. Внутреннее пространство граней заливается бетоном.
• Сборная лента. Данный тип фундамента не заливается раствором, а собирается из отдельных железобетонных фундаментных плит.

Разметка внешнего контура фундамента

Свайный фундамент

Если грунт, на котором строится дом слишком слабый чтобы удержать постройку, либо слишком неровный, разумным решением будет свайный фундамент.

Благодаря тому, что сваи проникают довольно глубоко, появляется возможность миновать слабые слои и поставить опору на более сильные. Сверху на сваи устанавливаются балки и стены, таким образом, получается устойчивый фундамент.

Сваи бывают следующих типов:

• Забивные. Массивные, длинные, армированные бетонные сваи с заостренным концом. Углубляется в грунт путем забивания с помощью специальной техники. Обычно не используется в частном строительстве небольших домов, так как использование техники, является довольно затратным удовольствием.
• Буронабивные. Вместо того чтобы вбивать готовые сваи, в грунте пробуриваются скважины, которые заполняются бетоном, высота верхушек которых регулируется в зависимости от плана постройки. Могут быть армированные или же неармированные.
• Винтовые. Металлические, заостренные сваи с винтами на конце. Это дает возможность более простым способом углубить их на необходимую глубину. Такой тип фундамента чаще используется в негабаритных частных постройках.

Плитный фундамент

Универсальный, надежный и самый дорогой тип фундамента. Монолитная железобетонная плита отливается на «подушке» под размер дома или немного больше. При движении грунта, подушка может плавать, что придает строению устойчивости.

Плитный фундамент может быть следующих типов:

• Мелкозаглубленный плитный фундамент. Устанавливается на поверхности грунта. Минусом такого фундамента является то что исключается возможность строительства подвала.
• Заглубленный плитный фундамент. При его строительстве вырывается яма с ровными стенами под размер дома, по дну выливается плита. При использовании данного фундамента возможно строительство подвала.

Схема разметки фундамента с учетом установленных норм расстояния до соседнего участка

Столбчатый фундамент

Является самым простым и дешевым, однако, и самым ненадежным фундаментом. Суть его заключается в том, что по периметру обозначения контуров стен устанавливаются невысокие столбы из кирпича, камней или бута. Устанавливаются они в наиболее ответственных местах, расстояние между ними от 1,2 до 2,5 метров.

Сверху устанавливается связующая балка, которая и формирует основу для будущего строения. Так же существует углубляющийся тип столбчатого фундамента. В местах основных опорных мест бурятся скважины, которые заливаются бетоном и армируются.

Снизу, для большей устойчивости, такие столбы расширены. Столбчатый фундамент устанавливается только на устойчивых фундаментах, и подходит лишь для малоэтажных, легких построек. Кроме того исключается строительство подвала.

Прямой угол — как вычислить подручными средствами

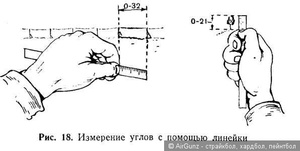Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.

Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.

В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.

Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.

В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве — не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.

Выравнивание углов стен

Раньше, когда ещё не было столько много инструментов и новых современных строительных материалов, выравнивание углов стен происходило следующим образом.

Бралась широкая деревянная доска, и прикладывалась к торцу дверного проёма или прямо к стене того угла, который необходимо было выровнять. Затем накидывался и разравнивался теркой цементный раствор на поверхность угла, то же самое происходило с другой его стороны.

Сегодня выравнивание углов стен можно выполнить совершенно иными способами, тем более что для этого существуют различные гипсовые смеси, работать с которыми одно удовольствие.

Инструменты для выравнивания углов стен

Какие бы углы стен, внутренние или наружные, неважно, нужно было бы выровнять, сначала перед этой работой необходимо подготовить следующий инструмент:

1.  Длинный строительный уровень.
2.  Обычные плоские шпателя и угловой шпатель.
3.  Миксер для размешивания раствора.

Из материалов для выравнивания углов стен своими руками потребуется гипсовая штукатурка (старт) и грунтовка.

Как выровнять внутренние углы стен

Выравнивание внутренних углов стен выглядит следующим образом. После грунтовки стен и приготовления шпаклёвочной смеси, раствор наносится плоским металлическим шпателем на внутренний угол небольшими порциями, расстояние между которыми должно быть приблизительно 15 сантиметров.

Далее берётся перфорированный уголок, который вдавливается в шпаклёвку, а её излишки сразу же убираются узким шпателем. Затем производиться выравнивание перфорированного уголка строительным уровнем.

Если внутренние углы стен имеют достаточную ровность, то можно для их выравнивания обойтись без использования перфорированного уголка. Для выполнения этой работы необходимо воспользоваться угловым шпателем и шпаклёвочной смесью.

Как выровнять наружные углы стен

Выравнивание наружных углов стен выполняется немного легче, поскольку здесь нет ограничений в свободе движения, а перфорированный уголок можно легко отклонять в ту или иную сторону, добиваясь максимальной ровности выравниваемого угла.

Схема выравнивания углов стен выглядит примерно такой же самой, как и при выравнивании внутренних углов. Если после замеров оказалось, так что вертикаль наружных углов сильно отклонена, то лучше воспользоваться перфорированным уголком.

При этом шпаклёвочная смесь набрасывается не на угол стены, который нужно выровнять, а на сам перфорированный уголок, приставленный к углу.

Выравнивание углов стен на самом деле несложная работа, которая вполне по силам даже новичкам в ремонте. А, учитывая «гибкость» в работе современных строительных смесей и наличие нужных инструментов для этого, процесс выравнивания углов становится вообще лёгким.

Вывод

Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.

При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.