Как посчитать площадь треугольника

Доборные элементы

Расчет дополнительной фурнитуры

Для полноценного монтажа необходима дополнительная фурнитура, так называемые доборные элементы. Такие детали можно приобрести как дополнительно, так и в комплекте с металлочерепицей. В первую очередь они необходимы для надежности кровли, в особенно ненадежных местах, а уже потом их можно рассматривать как часть декорации.

Элемент можно купить в среднем – 200 рублей за погонный метр. Но нужно подумать, что нам необходимо и для чего, а также подсчитать, во сколько это обойдется, в случае если придется покупать.

Итак, рассмотрим, нам необходимо:

1. Конек, планки торцевые, которые будут защищать от атмосферных явлений – дождь, ветер, и планка примыкания – для дополнительной герметизации различных стыков, к примеру, печной трубы. И это только самое необходимое, есть еще другие дополнительные детали, и они особенно необходимы, если система кровли сложная, многоскатная.
2. Барьер снеговой – для защиты водостока от внезапного обрушения снега, карнизная планка – защищает от попадания под конек пыли и грязи. Мы сейчас рассмотрим, как подсчитать самые необходимые комплектующие элементы, а потом исходя из расчетов, вы окончательно решите, что приобретать. Чтобы подсчитать количество фурнитуры нужно:
   • измерить длину конька, все будет зависеть, каких размеров будут планки, так как на стыки уходит 10 см, стандартный конек – 2 метра, к примеру, если длина конька 6 м, то понадобится покупать 4 планки, а это 800 рублей;
3. торцевые планки выпускаются разной длины, так и монтируются на торцевых скатах, высчитывается аналогичным образом, то есть с учетом, что на стыки должно уходить 10 см;
4. планка примыкания – рассчитывается по описанному выше принципу.

Кроме этого, необходимы саморезы стоимость их варьируется от 3 до 7 рублей за штуку. После подсчетов, можно подумать о цвете, если вы хотите, чтобы ваш дом выделялся и был виден издалека, то выбирайте любой яркий цвет. Качественно выполненная черепица не выгорает на солнце и не теряет своих качеств, и вы можете не беспокоиться, что со временем ваша крыша потеряет свой первоначальный вид.

Ориентировочная стоимость металлочерепицы

На просторах огромной России, стоимость любого продукта может значительно отличаться, металлочерепица не исключение. Разница в стоимости продукта не зависит от региона, а обуславливается в первую очередь от качества продукта и бренда производителя.

Например, в Москве на популярные марки металлочерепицы Монтерей, Супермонтерей и Макси стоимость равна на сегодняшний день — 250 рублей за кв. метр

А вот в Новосибирске те же марки обойдутся вам чуть дороже — 260 рублей, но с доставкой, что тоже немаловажно. Можно сделать заключение, что цена на продукт практически одинакова что в Сибири, что в столице, но с учетом доставки в Новосибирске немного выгоднее

Проверка урока! Допустим, получается, по вышеуказанному примеру, при 100 кв. м. крыши вам понадобится на закупку полотен, примерно 5250 рублей. Вы так по-прежнему считаете? Не забывайте, что нужно узнать размеры полотна, и вычислить полезную площадь.

Совет! Приобретайте продукт средней величины. На коротких листах получится малополезной площади, следовательно, нужно будет больше материала, значит, и средств.

Длинная металлочерепица экономнее в плане снижения отходов, но неудобна в установке. Рекомендуемый размер при самостоятельном строительстве 3620×1160 мм или 2220×1160 мм, но количество волн может быть разным. Консультант магазина может сказать точное число требуемых материалов, при условии, что вы будете знать значение площади покрытия. Теперь нужно сделать расчет дополнительной фурнитуры.

Вы здесь

Онлайн калькулятор — Учеба и наука — Математика — Геометрия — Геометрический калькулятор — Треугольник

Треугольник

Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.

Зная: Стороны треугольника	Зная: Два угла и сторону треугольника	Зная: Два угла и сторону треугольника «A»
Зная: Две стороны и угол треугольника	Прямоугольный треугольник	Зная: Катет и гипотенуза прямоугольного треугольника
Катет «B» и гипотенуза прямоугольного треугольника	Зная: Катет и угол прямоугольного треугольника	Катет «A» и угол «β» прямоугольного треугольника
Катет «B» и угол «α» прямоугольного треугольника	Катет «B» и угол «β» прямоугольного треугольника	Зная: Гипотенузу и угол прямоугольного треугольника
Гипотенуза и угол «β» прямоугольного треугольника	Равнобедренный треугольник	Зная: Высоту и сторону равнобедренного треугольника
Высота и сторона «B» равнобедренного треугольника	Зная: Сторону и угол равнобедренного треугольника	Сторона «A» и угол «β» равнобедренного треугольника
Сторона «B» и угол «α» равнобедренного треугольника	Сторона «B» и угол «β» равнобедренного треугольника	Зная: Высоту и угол равнобедренного треугольника
Высота и угол «β» равнобедренного треугольника	Равносторонний треугольник	Зная: Площадь равностороннего треугольника
Зная: Высоту равностороннего треугольника	Зная: Радиус вписанной окр. равностороннего треугольника	Зная: Радиус описанной окр. равностороннего треугольника
Зная: Основание и высоту треугольника

Метод Герона

Античный математик Герон Александрийский предложил свой способ получения квадратуры треугольника. Для вычислений достаточно знать длину трех его сторон, хотя сама методика достаточно сложна и не поддастся пятиклассникам:

1. Определите периметр: сложите отрезки сторон: a+b+c. Разделите число надвое. Полученные данные называются полупериметр (p) и имеют ключевое значение в геометрическом уравнении Герона.
2. Проведите вычисление по формуле: p (p — a) (p — b) (p — c). Т.е. сначала вычтите по отдельности длину каждой из сторон из значения полупериметра, а затем перемножьте между собой три полученных числа и сам полупериметр.
3. Извлеките корень из итогового значения. Искомая величина найдена.

Например, грани длиною 3, 4 и 5 см образуют полупериметр 6 см. После умножения согласно формуле получается значение 36. Корень из 36 равняется 6. Значит, 6 см2 — площадь этого треугольника. Для равносторонней фигуры расчет еще проще.

Равнобедренный треугольник и его площадь.

Если перед вами стоит задача вычислить формулу равнобедренного треугольника, то проще всего воспользоваться главной и как считается классической формулой площади треугольника.

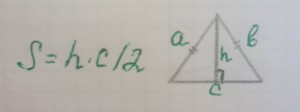
Но для начала, перед тем, как найти площадь равнобедренного треугольника, узнаем, что это за фигура такая. Равнобедренным треугольником называется треугольник, у которого две стороны имеют одинаковую длину. Эти две стороны называются боковыми, третья сторона называется основанием. Не путайте равнобедренный треугольник с равносторонним, т.е. правильным треугольником, у которого все три стороны равны. В таком треугольнике нет особых тенденций к углам, точнее к их величине. Однако углы у основания в равнобедренном треугольнике равны, но отличаются от угла между равными сторонами. Итак, первую и главную формулу вы уже знаете, осталось узнать, какие еще формулы определения площади равнобедренного треугольника известны:

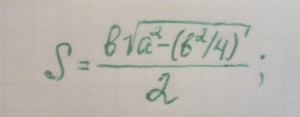
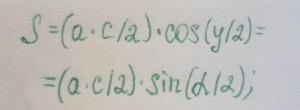
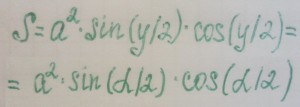
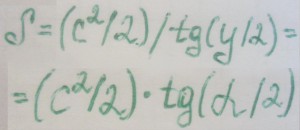
Как вы можете заметить, в этих формулах активно используются углы, их величины, косинусы, синусы и тангенсы. По этой причине, без специальной книжки вам не обойтись, хотя всю информацию вы сможете найти в Интернете. Отметим только, что в формулах угол альфа – тот, что находится между боковой стороной и основанием, а угол гамма (y) – тот, что находится между равными боковыми сторонами треугольника.

Как вычислить площадь треугольника

Треугольник – это такая геометрическая фигура, которая состоит из трех прямых, соединяющихся в точках, не лежащих на одной прямой.

Точки соединения прямых – это вершины треугольника, которые обозначаются латинскими буквами (например, A, B,C).

Соединяющиеся прямые треугольника называются отрезками, которые также принято обозначать латинскими буквами. Различают следующие типы треугольников:

• Прямоугольный.
• Тупоугольный.
• Остроугольный.
• Разносторонний.
• Равносторонний.
• Равнобедренный.

1

Общие формулы для вычисления площади треугольника

Формула площади треугольника по длине и высоте

S= a*h/2,где а — это длина стороны треугольника, площадь которого нужно найти, h-длина проведенной к основанию высоты.

Формула Герона

S=√р*(р-а)*(р-b)*(p-c),где √-это квадратный корень, p-полупериметр треугольника, a,b,c-это длина каждой стороны треугольника. Полупериметр треугольника можно вычислить по формуле p=(a+b+c)/2.

Формула площади треугольника по радиусу вписанной окружности и трем сторонам

S=p*r,где p-это полупериметр треугольника, площадь которого нужно найти, r-радиус вписанной в этот треугольник окружности.

Формула площади треугольника по трем сторонам и радиусу описанной вокруг него окружности

S= (a*b*c)/4*R,где a,b,c-это величина длины каждой стороны треугольника, R- радиус описанной вокруг треугольника окружности.

Формула площади треугольника по декартовым координатам точек

Декартовы координаты точек – это координаты в системе xOy, где x- это абсцисса, y- ордината. Декартовой системой координат xOy на плоскости называют взаимно перпендикулярные числовых оси Oх и Oy с общим началом отсчета в точке О.

Если заданы координаты точек на этой плоскости в виде A(x1, y1), B(x2, y2) и C(x3, y3), то можно вычислить площадь треугольника по следующей формуле, которая получена из векторного произведения двух векторов.

S = |(x1 – x3)•(y2 – y3) – (x2 – x3)•(y1 – y3)|/2,

где || обозначает модуль.

https://youtube.com/watch?v=ayOt9DwAsSQ

Прямоугольный треугольник – это такой треугольник, у которого один угол составляет 90 градусов. Такой угол у треугольника может быть лишь один.

Формула площади прямоугольного треугольника по катету и противолежащему углу

S = a*b/2*tg(β),где a, b – это катеты треугольника, tg(β) – это тангенс угла, в котором соединяются катеты a, b.

3

Как вычислить площадь равнобедренного треугольника

Равнобедренным называется такой треугольник, который имеет две равные стороны. Эти стороны называются боковыми, а другая сторона является основой. Для вычисления площади равнобедренного треугольника можно использовать одну из следующих формул.

Формула равнобедренного треугольника по боковой стороне и основанию

S=(c/2)* √(a*a – c*c/4),где с – основание треугольника, a- величина одной из боковых сторон равнобедренного треугольника.

Как найти площадь равностороннего треугольника

Равносторонний треугольник – это такой треугольник, у которого все стороны равны. Для вычисления площади равностороннего треугольника можно использовать следующую формулу: S = (√3*a*a)/4,

где a-это длина стороны равностороннего треугольника.

Вышеприведенные формулы позволят вычислить искомую площадь треугольника

Важно помнить, что для вычисления пощади треугольников нужно учитывать тип треугольника и доступные данные, которые можно использовать для вычисления

Для равнобедренного треугольника

Рассмотрим случаи нахождения площади, если у треугольника равные боковые стороны.

Через основание и сторону

 В этом случае формула будет выглядеть следующим образом:

\(S=\frac b4\sqrt{4a^2-b^2}\)

где a — одно из боковых ребер фигуры, а b — ее основание.

Через основание и противолежащий угол

Зная длину основания и противолежащий ему угол, мы можем использовать следующую формулу:

\(S=\frac{b^2}{4\tan\left({\displaystyle\frac\beta2}\right)}\)

где b — основание многоугольника, β — противолежащий ему угол.

Через основание и высоту

Если нам известна величина основания равнобедренного треугольника, а также его высота, найдем S по приведенной ниже по элементарной формуле:

\(S=\frac{b\times h}2\)

где b — основание фигуры, а h — высота, проведенная к этому основанию.

Через боковые стороны и угол между ними

Если мы знаем длину боковых сторон и угол между ними, найдем площадь, опираясь на расчеты:

\(S=\frac12a^2\times\sin\left(\beta\right)\)

где a — это боковое ребро, β — угол между равными ребрами.

Через основание и угол между боковыми сторонами

В этом случае нам сначала придется найти высоту по формуле:

\(h=\frac b2\tan\left(\beta\right)\)

где β — угол при вершине, а b — основание.

Далее подставляем значение в формулу

\(S=\frac{b\times h}2 = \frac{b\times{\displaystyle\frac b2}\tan\left(\beta\right)}2=\frac{b^2\tan\left(\beta\right)}4\)

Итоговая формула:

\(S=frac{b^2\tan\left(\beta\right)}4\)

Свойства треугольника

1. длина любой стороны треугольника меньше суммы длин двух остальных сторон, но больше разницы длин двух остальных сторон;
2. высота треугольника образует прямой угол со стороной, к которой проведена;
3. площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота S_ABC=a⋅h/2.

Пример. Можно ли построить треугольник из отрезков с длинами: 3 см, 7 см, 4 см?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. 3 + 4 = 7, значит построить треугольник не получится.

Пример. Можно ли построить треугольник из отрезков с длинами: 16 см, 32 см, 18 см?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. Так как для укаанных длин будут справедливы следующие равенства: 16 + 18 > 32 и 16 > 32 − 18, то треугольник построить получится.

Пример. Можно ли построить треугольник из отрезков с длинами: 1 см, 3 см, 7 см ?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. 3 + 1

Пример. Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 4 см, другая сторона, которая образует прямой угол, в 2 раза меньше. Определи площадь треугольника.

Пусть AB = 4 см, тогда сторона BC = 4 : 2 = 2. И тогда площадь треугольника будет равна: S = 2 * 4 : 2 = 4 см2

Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 12 см, другая сторона, которая образует прямой угол, в 3 раза меньше. Определи площадь треугольника.

Пусть AB = 12 см, тогда сторона BC = 12 : 3 = 4. И тогда площадь треугольника будет равна: S = 12 * 4 : 2 = 24 см2

Рассчитай площадь треугольника ABC, если дана площадь клетки — 1 м2.

В треугольнике от вершины B проведём перпендикуляр к стороне AC. Таким образом данный треугольник разбит на два прямоугольных треугольника. Каждый из них — половина прямоугольника.

Поэтому площадь можно рассчитать следующим образом:

S_ABC=4⋅4/2+3⋅4/2=(16+12)/2=28/2=14м2.

Известно, что периметр равностороннего треугольника — 21 см. Определи периметр данного четырёхугольника, который состоит из равносторонних треугольников.

Известно, что периметр равностороннего треугольника — 21 см.

Значит, одна сторона треугольника равна 7 см.

Периметр данного четырёхугольника состоит из 4 таких сторон, значит, равен 28 см.

Дан равносторонний треугольник. 2 раза сделано следующее:

1. на всех сторонах отмечены и соединены серединные точки. 2. На сторонах внутреннего треугольника опять отмечены и соединены серединные точки. Треугольник, который образовался на этот раз, закрашен розовым цветом.

Внутренний треугольник состоит из 4 маленьких треугольников, такими же являются остальные 3 треугольника, следовательно, всего 4⋅4=16 маленьких треугольников.

2. Чему равна площадь большого треугольника, если площадь розового треугольника равна 4 м²?

Площадь большого треугольника равна 16⋅4=64 м².

3. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 4 раза?

Очевидно, что в каждой следующей конструкции число маленьких треугольников увеличивается в 4 раза.

Если повторить эти действия (построить такую конструкцию) 4 раза, то общее число маленьких треугольников будет равняться 256.

4. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 3 раза?

Очевидно, что в каждой следующей конструкции число маленьких треугольников увеличивается в 4 раза.

Если повторить эти действия (построить такую конструкцию) 3 раза, то общее число маленьких треугольников будет равняться 64.

Определи площадь данных фигур, если площадь одной клетки равна 6 см2. 1)

Фигура образует 2 клетки, а ее площадь равна 6 *2 = 12 кв.см.

У второй фигуры будет 8 клеток. Площадь фигуры равна 8 ⋅ 6 = 48см2 .

Подумай, как построены данные фигуры, и определи, сколько клеток будет у следующих двух фигур, если их построить по той же закономерности.

У третьей фигуры — 18 клеток, у четвертой — 32 клетки.

Калькулятор площади треугольника по трем сторонам

Как известно, треугольником принято называть плоскую геометрическую фигуру, многоугольник, который ограничен минимальным количеством сторон. Также, стоит помнить, что всякий многоугольник делится на определённое количество треугольников.

Для этого необходимо соединить его вершины такими отрезками, которые не пересекали бы его стороны. Вот почему, зная как рассчитать площадь треугольника, Вы можете получить площадь большинства геометрических фигур.

Формула Герона для вычисления площади треугольника по трем сторонам

В том случае если нам известны параметры каждой стороны нашего треугольника, мы можем рассчитать площадь фигуры по формуле Герона. Для её упрощения следует применить новую величину, так называемый полупериметр, который является суммой всех сторон треугольника, которая разделена пополам.

После получения значения полупериметра, Вы можете приступать к расчёту площади по руководствуясь следующей формулой: S = sqrt(p(p-a)(p-b)(p-c)), в которой «p» – полупериметр, «a,b,c» – стороны фигуры и sqrt –квадратный корень.

Пример вычисления площади треугольника по трем сторонам

Рассмотрим на примере вычисление площади треугольника по формуле Герона.

p = (a + b + c)/ 2  где p – половина периметра треугольника.

таким образом S = √ p ( p – a ) ( p – b ) ( p – c ) .

(Это также называется формулой Герона)

Дано:

Треугольник со сторонами a = 4, b = 5, c = 3.

Задание:Найдите площадь треугольника

Решение:

Используйте формулу половинного периметра:

p = (3 + 4 + 5)/ 2= 6

Полученные значения подставляем в формулу Герони:

S = √ 6 ( 6 – 3 ) ( 6 – 4 ) ( 6 – 5 ) =

√ 6 ⋅ 3 ⋅ 2 ⋅ 1 = √ 36 =6

Ответ: 6

Историческая справка

Формула приписывается Герону, живущему в  Александрии, который был греческим инженером и математиком в 10 – 70 годах нашей эры

Среди прочего, он разработал  первый известный паровой двигатель, но его рассматривали как игрушку!

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м.  В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту

Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный

Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка

Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Вычисления с помощью окружностей

На практике используются способы расчета площади треугольника с помощью вписанной или описанной окружности. В первом случае необходимо знать величины всех сторон и радиус вписанного элемента. Далее:

• найдите полупериметр (p);
• умножьте полученную величину на значение радиуса (r) окружности и получите площадь.

Совет. При неизвестном радиусе его рассчитывают по формуле: r = P/2π. P — длина окружности, π — математическая константа.

По описанной вокруг треугольника окружности также можно вычислить его площадь. Потребуется знать радиус:

• получите произведение всех сторон треугольника;
• умножьте радиус на 4;
• разделите первое значение на второе.

Важно! Формула:

Пример для треугольника со сторонами 3,4 и 5 см. Если описать окружность, касающуюся каждой его вершины, то ее радиус будет равняться 2,5. После подстановки величин в уравнение получите итоговое значение 6 см2.

Предложенный набор методов — базовый, но вовсе не исчерпывающий. Существуют более сложные способы решения задания с меньшим количеством вводных данных и многоступенчатым расчетом.

Как узнать площадь окон и дверей?

Площадь, занятая окнами, измеряется по откосам и подоконнику. Высота окна определяется по боковому откосу, ширина – по подоконнику или верхнему откосу.

Например, ширина окна – 1,55 м, высота – 1,65 м.

1,65 х 1,55 = 2,56 м2

Если окон несколько, общая площадь их суммируется.

Площадь треугольного окна: S = 0,5А*h, где А – нижняя сторона/ширина окна, h – высота.

Если ширина треугольного окна 2 метра, а высота – 1,5 метра, то площадь окна составит:

0,5 х 1,5 х 2 = 1,5 м2.

Площадь дверей, также как и площадь прямоугольной стены, измеряется простым умножением ширины двери на высоту. За основу берутся снятые замеры по коробке, а не по полотну.