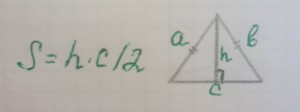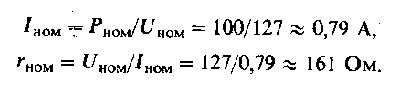Фигура треугольник в техническом анализе: стратегия торговли

Знамя Мира

У символа из трех кругов или точек очень широкая область интерпретаций, во многом аналогичная с равносторонним треугольником. Самым известным вариантом знака стало Знамя Мира, дизайн которого был разработан русским художником, философом и писателем Рерихом Николаем Константиновичем для международного Пакта защиты культурного наследия в 1935 году.

Описание и цель применения символа в официальном договоре приводится таким образом:

О том, насколько знак распространен в религиозной культуре разных народов и что вдохновило художника на идейное и визуальное содержание Знамени Мира, сам Рерих говорит в своих письмах и записях, изданных в двухтомном собрании «Листы дневника»:

[править] Типы треугольников

Треугольники можно классифицировать в зависимости от относительной длины его сторон:

• В равностороннем треугольнике все стороны имеют одинаковую длину. Все углы равностороннего треугольника также одинаковы и равны 60°. Равносторонний треугольник еще называют правильным.
• В равнобедренном треугольнике две стороны имеют одинаковую длину, третья сторона при этом называется основой треугольника. Равнобедренный треугольник имеет два одинаковых угла, которые находятся при его основе.
• Разносторонний треугольник имеет стороны разной длины. Внутренние углы разностороннего треугольника разные.

Также треугольники можно классифицировать в соответствии с их внутренними углами:

• Прямоугольный треугольник имеет один внутренний угол равный 90° (прямой угол). Сторона, противоположная прямому углу, называется гипотенуза. Другие две стороны называются катетами прямоугольного треугольника.
• Тупоугольный треугольник имеет один внутренний угол больше 90°.
• В остроугольном треугольнике все углы меньше 90°. Равносторонний треугольник является остроугольным, но не все остроугольные треугольники равносторонние.

Треугольник Рёло — это выпуклый криволинейный треугольник, получаемый при пересечении трёх окружностей одного радиуса с центрами в вершинах правильного треугольника со стороной равной радиусу.

Прямоугольный треугольник

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла. 

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$. (Рис.14)
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника. (Рис.14)

Один острый угол прямоугольного треугольника на $44°$ больше другого острого угла. Найдите больший острый угол.

Решение:

В прямоугольном треугольнике $АВС$ $∠А$ и $∠В$ – острые.

Пусть $∠ А – х$, тогда $∠ В — (х+44)$.

Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

На основании этого правила, составим и решим уравнение:

$х+х+44=90$

$2х+44=90$

$2х=90-44$

$2х=46$

$х=23$

Угол $В$ больший в этом треугольнике, через $«х»$ он записывался как, $х+44$, следовательно, $∠В=23+44=67°$.

Ответ: $67$

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. 

$АС^2+ВС^2=АВ^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$ 

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
5. Основное тригонометрическое тождество: $sin^2x+cos^2x=1$
6. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
7. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
8. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

[править] Точки и линии, связанные с треугольником

Есть сотни различных построений для определения особых точек внутри треугольника, которые удовлетворяют некоторым уникальным условиям. Часто необходимо построить три прямые, связанные аналогично с тремя сторонами (вершинами, углами) треугольника и тогда убедиться, что они пересекаются в одной точке. Важным инструментом для проверки этого является теорема Чевы, которая дает критерии для определения конкурентности прямых. Подобно этому, линии, связанные с треугольником часто строятся после проверки, три аналогичным образом полученные точки является коллинеарными — теорема Менелая дает для этого случая общий критерий. В этом разделе приведены только такие построения, которые наиболее часто встречаются.

Центр описанной окружности.

Срединный перпендикуляр треугольника — это перпендикуляр, который проходит посередине стороны треугольника. Три срединных перпендикуляра пересекаются в одной точке, которая является центром описанной окружности. Диаметр описанной окружности можно определить из теоремы синусов.

Исходя из теоремы Фалеса, можно утверждать, что если центр описанной окружности расположен на одной из сторон треугольника, тогда противоположный угол прямой. Более того, если центр описанной окружности находится внутри треугольника, то треугольник остроугольный, а если наружу, то треугольник тупоугольный.

Три высоты треугольника пересекаются в ортоцентре.

Высота треугольника — прямая, проведенная из вершины и перпендикулярная к противоположной стороне или к продолжению противоположной стороны. Эта сторона называется основанием треугольника. Точка пересечения стороны и перпендикуляра называется основой перпендикуляра. Длина высоты — это расстояние от вершины к основанию треугольника. Три высоты пересекаются в одной точке, которая называется ортоцентром треугольника. Ортоцентр лежит внутри треугольника (и соответственно все основания перпендикуляров лежат в треугольнике) тогда и только тогда, когда треугольник не тупоугольный.

На пересечении двух биссектрис треугольника находится центр вписанной окружности.

Биссектриса треугольника — это прямая, проведенная через вершину, которая делит соответствующий угол на две равные части. Три биссектрисы пересекаются в одной точке, инцентре, центре вписанной в треугольник окружности. Вписанная окружность — это круг, который лежит внутри треугольника и примыкает к трем его сторонам. Кроме того, есть еще три важных круга, внешние вписанные; они лежат за пределами треугольника и соприкасаются с одной его стороной, а также к продолжению других двух. Центры внутреннего и внешних вписанных кругов образуют ортоцентрическую систему.

Барицентр — центр масс треугольника.

Медиана треугольника — это прямая, проведенная через вершину и середину противоположной стороны и делящая треугольник на две одинаковых площади. Три медианы пересекаются в одной точке, которая называется центроидом треугольника. Эта точка также центр масс треугольника: если бы треугольник был сделан из дерева, то можно было бы держать равновесие держась за центроид. Центроид делит каждую медиану в соотношении 2:1, например расстояние между вершиной и центроидом вдвое больше, чем между центроидом и противоположной стороной.

Окружность девяти точек.

Средние точки трех сторон и основы трех высот лежат на одном круге, который называется кругом девяти точек треугольника. Остальные три точки, из-за которых круг получил свое название, это середины той части высоты, лежащей между ортоцентром и вершиной. Радиус окружности девяти точек равен половине описанной окружности. Она соприкасается со вписанной окружностью (в точке Фейербаха) и с тремя внешними вписанными кругами.

Первый признак равенства треугольников

Теорема:

Два треугольника равны, если у них равны две стороны и угол, лежащий между этими сторонами.

Доказательство:

Рассмотрим два треугольника  ABC  и  A₁B₁C₁,  у которых:

 AB = A₁B₁,  AC = A₁C₁,  ∠A = ∠A₁.

Требуется доказать, что

ABC = A₁B₁C₁.

Если наложить  A₁B₁C₁  на  ABC  так, чтобы точка  A₁  совместилась с точкой  A  и сторона  A₁B₁  совместилась со стороной  AB,  то точка  B  совместится с точкой  B₁,  так как  A₁B₁ = AB.  Сторона  A₁C₁  совместится со стороной  AC,  так как  ∠A = ∠A₁.  Точка  C₁  совпадёт с точкой  C,  так как  A₁C₁ = AC.  Стороны  B₁C₁  и  BC  совместятся, так как совместились их концы. Таким образом, треугольники совместятся. Теорема доказана.

Как можно улучшить свои результаты в торговле треугольников?

Первая и самая важная вещь – это таймфреймы, которые вы будете использовать. Держитесь подальше от низких таймфреймов и внутридневного шума, который может возникнуть в результате незначительных новостных событий и случайных колебаний цены. Также на более старших таймфреймах ложные пробои гораздо более редки.

У вас появится гораздо больше времени для принятия торговых решений. Вы будете меньше волноваться и сможете спокойно найти оптимальную точку входа и определиться с целями по взятию прибыли.

Заключайте меньшее количество сделок. Если вы торгуете по дневным таймфреймам и совершаете более десяти сделок в месяц, существует 90% вероятность, что вы торгуете слишком часто. Другими словами, вы выбираете количество, а не качество. Когда речь заходит о лучших точках входа – их всегда будет не так много. По моему опыту, это число колеблется от трех- четырех до, возможно, десяти в течение активного месяца.

Прежде чем добавлять треугольник в свой торговый арсенал, вам придется набраться терпения. Не ожидайте появления этой фигуры каждую неделю или даже каждый месяц. Однако при правильном соотношении риска к прибыли потенциальный доход может оправдать все ваши ожидания.

Постоянно отслеживайте свои результаты, как хорошие, так и плохие. Отслеживать свои ошибки гораздо важнее, чем ваши успехи. Несмотря на то, что иногда это утомительно и даже скучно, ведение торгового журнала является решающим шагом для становления прибыльного трейдера.

Троица и треугольник

Начиная с ранних христиан треугольник был символом Святой Троицы. Равносторонний треугольник толковался как равенство и единая божественная сущность Бога Отца, Бога Сына и Духа Святого. Иногда этот символ составляли из трех переплетенных между собой рыб. Символ Троицы по католической традиции составлялся из трех малых треугольников, вписанных в один большой с кругами на вершинах. Три этих круга означают триединство, но каждый круг независим и совершенен сам по себе. Эта схема иллюстрировала принцип триединства и вместе с тем индивидуальности каждого составляющего Святой Троицы.

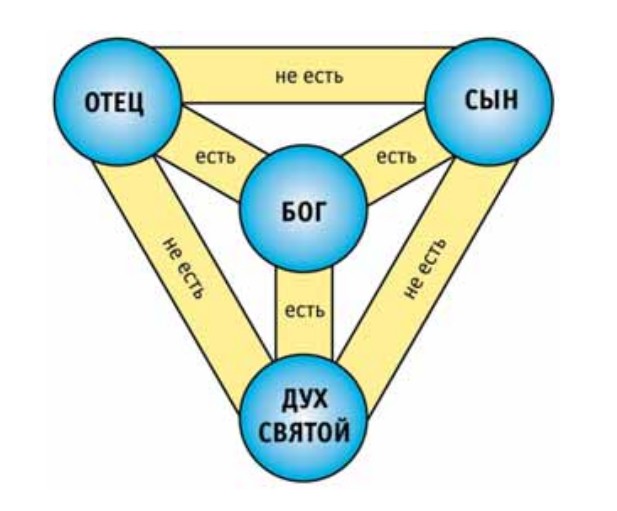Схема Святой Троицы по католической традиции

Треугольники как символ Троицы в готической архитектуре

Христианские варианты треугольника

В религиозной символике Средневековья появлялось много разновидностей подобных фигур:

1. Треугольник в сочетании с крестом символизировал смерть на кресте Иисуса за грехи человеческие, воскресение его Богом-Отцом, покаяние христиан и снисхождение Святого Духа.
2. Три рыбы, составляющие треугольник, означали: Иисус Христос, Сын Божий, Спаситель. Также они знаменовали Троицу.
3. Треугольник, содержащий греческие буквы Omicron, Omega и Nu. Эти буквы означают собой слова εγω ειμι ο ων, сказанные Богом Моисею из горящего куста (Исход 3:14), которые переводятся как «Я есть Сущий». Дословно фраза была взята из Септуагинты, древнегреческого перевода Ветхого Завета.
4. Три фигурки бегущих кроликов создают два треугольника, внутренний и внешний. Символ часто присутствовал как рельефный элемент архитектуры и деревянных деталей. Знак также знаменует Триединого Бога. Такое изображение встречается в настенной живописи древнего Египта и, возможно, тогда символизировало мужчину, женщину, потомство.

Заключительное слово

Что бы ни говорили противники описанного метода измерений, но «египетский треугольник» в значительной степени помогает строителям в выведении прямых углов. Конечно, при условии его правильного использования. Тем более что навязать 12 узлов на верёвке на определённом расстоянии один от другого много времени не потребует. Также это не потребует и финансовых затрат, связанных с наймом геодезиста с необходимым оборудованием.

ФОТО: profipol.dp.uaТак должны быть расположены узлы на верёвке для построения «египетского треугольника»

Watch this video on YouTube

Предыдущая DIY HomiusПрочные хомуты из ПЭТ-бутылки за минуту
Следующая DIY HomiusСмеяться или плакать: ошибки во время ремонта

Созвездие Треугольника

Точное происхождение названия этого созвездия неизвестно. Свое название оно получило на Древнем Востоке, его знали и использовали в навигации финикийские мореходы. Для них оно символизировало священный камень пирамидальной формы. Треугольник входил в число 48 классических созвездий античности. Древние греки считали, что это — перенесенная на небо дельта Нила, что указывает на египетские корни названия созвездия. Уже в Новое время на звездном небе были выделены созвездия Южного Треугольника и Наугольника.

Созвездие Треугольника. Иллюстрация из астрономического атласа «Уранография» Я. Гевелия

Пример задачи на использование 4 замечательных точек треугольника

Пример 1

Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что

а) точка $D$ — середина стороны $BC$.

б) $\angle A=\angle B+\angle C$

Решение.

Изобразим рисунок.

Рисунок 5.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.

б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$\angle A=\angle DXB$, как соответственные углы. Значит, $\angle A={90}^0$. Тогда$\angle B+\angle C={180}^0-\angle A={180}^0-{90}^0={90}^0=\angle A$

ч. т. д.

Точка пересечения медиан треугольника

Теорема 1

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

Рассмотрим треугольник $ABC$, где ${AA}_1,\ {BB}_1,\ {CC}_1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $\angle ABB_1=\angle BB_1A_1,\ \angle BAA_1=\angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Теорема доказана.

Элементы остроугольного треугольника:

Кроме сторон и углов у одностороннего треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. остроугольного, 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым углом.

Рис. 4. Остроугольный треугольник и внешний угол

∠ ВСD – внешний угол

Медиана остроугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 5. Остроугольный треугольник и медиана остроугольного треугольника

MС – медиана остроугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 6. Остроугольный треугольник и высота остроугольного треугольника

MС – высота остроугольного треугольника

Высота остроугольного треугольника находится внутри треугольника. Все 3 высоты остроугольного треугольника (как и любого треугольника) пересекаются в одной точке, называемой ортоцентром.

Биссектриса в остроугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

Рис. 7. Остроугольный треугольник и биссектриса угла остроугольного треугольника

MС – биссектриса угла остроугольного треугольника

Кроме того, биссектриса остроугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Еврейский символ

Один из исследователей еврейских и иудейских символов Ури Офир цитирует раввина Моше Файнштейна, который в респонсе «Игрот Моше» указывает, что истоки Звезды Давида, как еврейского символа, неизвестны. Тем не менее он выдвигает версию, что происхождение Звезды Давида связано с храмовой менорой. Под каждым из её семи светильников располагался цветок: «И сделай светильник из золота чистого; чеканный да сделан будет светильник; бедро его и стебель его, чашечки его, завязи его и цветы его должны быть из него». Ури Офир считает, что это был цветок белой лилии, который по форме напоминает Маген Давид.

Тату-треугольник на коленях: идеи, фото, значения

Треугольник со звездой – это тату-треугольник стоит наносить в знак своей исключительности. Корни подобного отношения к символу-звезде уходят глубоко – во времена, когда его наносили лишь избранные люди. Шаманы, например. А объединяющий все аспекты жизни треугольник подчеркнет, что хозяин татуировки чувствует себя уверенно во всех сферах жизни.

Подобную тату стоит нанести людям, которым необходимо вдохновение. Ведь звезды ассоциируются с небом, с полетом мысли и легкостью. Также звездочки издревле помогали путникам найти верную дорогу, что в переносном смысле при поиске себя весьма полезно.

Тату на колене выглядит эффектно

Паутинку можно составить из треугольников. Во-первых, потому, что геометрическое тату достаточно популярно в последнее время. Во-вторых, объединение всех жизненных этапов в данном случае очень актуально. Таким образом человек подчеркнет, что его принципы были неизменными всегда и останутся таковыми.

Тату-паутина из треугольников

Геометрические татуировки в последнее время приобретают все большую популярность. Они стильные, лаконичные, философские и универсальные одновременно. Надеемся, что наши читатели найдут что-нибудь и для себя.

Как пользоваться валькнутом в качестве оберега

Значение валькнута в повседневном обиходе – стремление к познанию.

Его носят для погружения в тайны окружающего мира и поиска собственного жизненного смысла.

Также талисман способен развивать у носителя способности к ясновидению и логическому мышлению.

Одновременно он оптимизирует когнитивные функции (память, внимание и т. д.)

Но одновременно с вышеперечисленным такой талисман опасен тем, что призывает на носителя серьезные испытания.

Если человек, носящий этот знак, выдержит свалившиеся на него невзгоды, ему даруется доступ к потаенным знаниям.

Используется валькнут в виде всевозможных украшений: браслет валькнут, кулоны, кольца, перстни, сережки, подвески.

Также до сих пор распространена практика нанесения этого знака на тело в качестве татуировки.

Глаз в треугольнике

Символ, графически представляющий собой вписанный в треугольник глаз, называемый «глазом провидения» или «всевидящим оком», появился в Европе в XVII в. Считается, что он восходит к солярному глазу Гора древних египтян. Этот знак получил широкое распространение в барочной архитектуре, украшая фронтоны роскошных католических костелов.

В XIX в. он появился и на православных храмах, например, на фронтоне Казанского собора в Санкт-Петербурге. Христианство рассматривало его как символ Святой Троицы. Одновременно этот символ использовался и масонами, которые трактовали его как символ абсолюта, просвещения и высшего знания. У масонов «глаз провидения» располагается над стулом мастера ложи, чтобы таким образом напоминать о всепроникающей во все тайны мудрости Творца.

Декларация прав человека и гражданина, Франция, конец XVIII в.

Герб белорусского города Браслав

Свойства равностороннего треугольника:

1. В равностороннем треугольнике все стороны равны между собой.

2. В равностороннем треугольнике углы равны и составляют 60°.

3. В равностороннем треугольнике каждая медиана, проведенная к каждой стороне, является биссектрисой и высотой, и они равны между собой.

В равностороннем треугольнике биссектриса, проведенная к каждой стороне, является медианой и высотой, и они равны между собой.

В равностороннем треугольнике высота, проведенная к каждой стороне, является биссектрисой и медианой, и они равны между собой.

Рис. 2. Равносторонний треугольник

АK = BF = CD

4. В равностороннем треугольнике высоты, биссектрисы, медианы и серединные перпендикуляры пересекаются в одной точке, которая называется центром равностороннего треугольника. Она же является центром вписанной и описанной окружностей.

Рис. 3. Равносторонний треугольник

R – радиус описанной окружности, r – радиус вписанной окружности

5. В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной.

6. Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, если считать от вершин.

Рис. 4. Равносторонний треугольник

AO : OK = BO : OА = CO : OD = 2 : 1

Понятие треугольника

Вспомним следующую аксиому для такого основного понятия геометрии, как прямая.

Аксиома 1: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.

Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда

Определение 1

Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.

Определение 2

Точки в рамках определения 1 называются вершинами треугольника.

Определение 3

Отрезки в рамках определения 1 называются сторонами треугольника.

Треугольник будем обозначать тремя точками его вершин (рис. 1)

Треугольник Кеплера

В начале XVII в. знаменитый астроном Кеплер составил диаграмму соединения планет Сатурна и Юпитера. Так в астрономии называют расположение планет, при котором для земного наблюдателя эклиптические долготы равны нулю, а сами небесные тела находятся близко друг к другу или даже перекрываются. Кеплер представил это явление в виде треугольника, который вращается по зодиакальному кругу, совершая полный оборот за 2400 лет.

Великий треугольник соединения Сатурна и Юпитера

Четыре стихии: Земля, Вода, Воздух и Огонь. Миниатюра из алхимического трактата XVII в.

Рождение Сына Солнца из Философского яйца. Миниатюра из алхимического трактата XVII в.

Король Земли поклоняется философской сере. Миниатюра из алхимического трактата XVII в.

Свойства остроугольного треугольника:

Свойства остроугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 8. Остроугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 9. Остроугольный треугольник с равными боковыми сторонами

АВ = ВС

3. Сумма углов остроугольного треугольника равна 180°.

4. Любая сторона остроугольного треугольника меньше суммы двух других сторон и больше их разности:

• • a < b + c;
  • a > b – c;
  • b < a + c,
  • b > a – c;
  • c < a + b;
  • c > a – b.

Примечание:  Фото https://www.pexels.com, https://pixabay.com

карта сайта

Коэффициент востребованности
1 790

Равносторонний треугольник (понятие, определение):

Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют 60°.

Равносторонний треугольник называется также правильным или равноугольным треугольником.

По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним). Иными словами, правильный (равносторонний) треугольник является частным случаем равнобедренного треугольника.

Рис. 1. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника, ∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника

Что это такое?

Треугольником называется музыкальный инструмент с палочкой в комплекте, который относится к числу самых элементарных ударных. Своё название он получил из-за своей формы в виде равностороннего треугольника. В народе на Руси его называли не иначе как «трензель», однако столь необычное название в оркестре не прижилось.

В целом этот инструмент представляет собой прут из металла, который изогнут в нужную форму. При этом в одном из углов этого треугольного инструмента концы металлического прута не сходятся, то есть получается, что этот угол остаётся открытым.

Несмотря на визуальную простоту инструмента, производят его по строгим правилам, дабы не исказить его звучания. Для его создания задействуют особый вид стали – серебрянку

Большое внимание уделяют и палочке инструмента

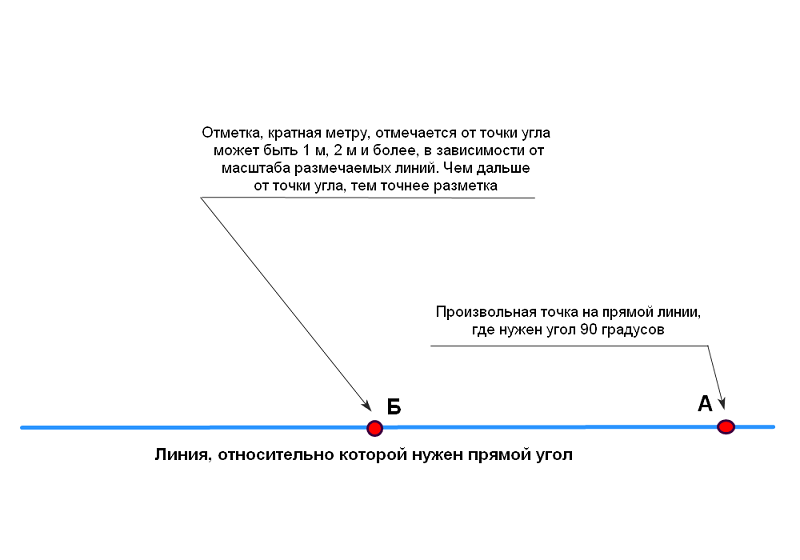
Иные способы выведения прямого угла

Если нет желания заниматься выведением углов самостоятельно, а финансы позволяют обратиться за помощью к специалистам, можно вообще не думать об этом вопросе. Один звонок − и на участке уже находится геодезист с теоделитом, который в сжатые сроки сделает разметку. Однако в этом случае необходимо быть готовым к внушительным затратам на оплату его труда.

ФОТО: omegagalvanoplastia.com.brТеоделит – высокоточная техника, однако стоимость подобной разметки может влететь «в копеечку»

Если говорить о минимальных затратах, то, основываясь на прайс-листах фирм, оказывающих подобные услуги, вызов и работа геодезиста с инструментом обойдётся в 1 000 руб./час при минимальной оплате 7 000 руб. Дальше − больше. Разметка осей (2 точки) – ещё 3 000 рублей. Если же потребуется определить точные координаты по GPS, то здесь каждые три точки обойдутся владельцу в 5 000 руб. Можно посчитать, какова будет общая сумма (все цены указаны с учётом на конец сентября 2020 года). Не проще ли самому произвести все необходимые разметки? Ведь сэкономленные средства всегда можно потратить на что-то полезное в дальнейшем строительстве.

ФОТО: thelundreport.orgСтоит приготовиться к тому, что карман значительно облегчится